练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．根据如表样本数据
    x3456
    y2.5t44.5
    得到回归方程y=0.7x+0.35，则t=（　　）
    A．2.6B．2.8C．2.9D．3

    分析 根据已知表中数据，可计算出数据中心点（$\overline{x}$，$\overline{y}$）的坐标，根据数据中心点一定在回归直线上，将（$\overline{x}$，$\overline{y}$）的坐标代入回归直线方程y=0.7x+0.35，解方程可得m的值．

    解答 解：由已知中的数据可得：$\overline{x}$=（3+4+5+6）÷4=4.5，$\overline{y}$=（2.5+t+4+4.5）÷4=$\frac{11+t}{4}$，
    ∵数据中心点（$\overline{x}$，$\overline{y}$）一定在回归直线上，
    ∴$\frac{11+t}{4}$=0.7×4.5+0.35，
    解得t=3，
    故选：D．

    点评 本题考查的知识点是线性回归方程，其中数据中心点（$\overline{x}$，$\overline{y}$）一定在回归直线上是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．如图，某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k，则水深从最小值变化到最大值至少需要（　　）
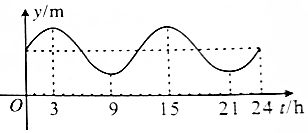
    A．6hB．8hC．12hD．24h

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知△ABC三个内角A、B、C所对的边分别为a、b、c，且3sinA=a，sinB=$\frac{3}{4}$，则b等于（　　）
    A．$\frac{9}{4}$B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．关于函数f（x）=tan（2x-$\frac{π}{4}$），有以下命题：
    ①函数f（x）的定义域是{x|x≠$\frac{1}{2}$kπ+$\frac{3π}{8}$，k∈Z}；
    ②函数f（x）是奇函数；
    ③函数f（x）的图象关于点（$\frac{π}{8}$，0）对称；
    ④函数f（x）的一个单调递增区间为（-$\frac{π}{2}$，$\frac{π}{2}$）．
    其中，正确的命题序号是①③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知定认在R上的可导函数f（x）的导函数f′（x），若对于任意实数x，有f′（x）＜f（x），且y=f（x）-1为奇函数，则不等式f（x）＜ex的解集为（　　）
    A．（0，+∞）B．（-∞，0）C．（-∞，e4）D．（e4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．为了对2016年某校中考成绩进行分析，在60分以上的全体同学中随机抽取8位，他们的数学、物理、化学分数（折算成百分制）事实上对应如表：
    学生编号12345678
    数学分数x6065707580859095
    物理分数y7277808488909395
    化学分数z6772768084879092
    （1）若规定80分以上为优秀，请填写如下2×2列联表，问是否有90%的把握认为是否优秀与科目有关；
      优秀 不优秀 合计
     数学   
     物理   
     合计   
    （2）用变量y与x，z与x的相关系数说明物理与数学、化学与数学的相关程度；
    （3）求y与x，z与x的线性回归方程（系数精确到0，01），当某位同学的数学成绩为50分时，估计其物理、化学两科的成绩．
    参考公式：相关系数r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}•\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$，
    回归直线方程是：$\widehat{y}$=bx+a，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$，
    参考数据：$\overline{x}$=77.5，$\overline{y}$=85，$\overline{z}$=81，$\sum_{i=1}^{8}$（xi-$\overline{x}$）2≈1050，$\sum_{i=1}^{8}$（yi-$\overline{y}$）2≈456，$\sum_{i=1}^{8}$（zi-$\overline{z}$）2≈550，≈688，$\sum_{i=1}^{8}$（xi-$\overline{x}$）（zi-$\overline{z}$）≈755，$\sqrt{1050}$≈32.4，$\sqrt{456}$≈21.4，$\sqrt{550}$≈23.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设两个非零向量$\overrightarrow{a}$，$\overrightarrow{b}$不共线．
    （1）如$\overrightarrow{AB}$=$\overrightarrow{a}$+2$\overrightarrow{b}$，$\overrightarrow{BC}$=-3（$\overrightarrow{a}$-$\overrightarrow{b}$），$\overrightarrow{CD}$=-2$\overrightarrow{a}$-13$\overrightarrow{b}$，求证：A，B，D三点共线．
    （2）试确定k的值，使k$\overrightarrow{a}$+12$\overrightarrow{b}$和3$\overrightarrow{a}$+k$\overrightarrow{b}$共线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在矩形ABCD中，AB=2AD=2$\sqrt{2}$，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM；
    （1）求证：AD⊥BM
    （2）若点E是线段DB上的一点，问点E在何位置时，二面角E-AM-D的余弦值为$\frac{\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．某个命题与正整数有关，若当n=k（k∈N*）时该命题成立，那么可推得当n=k+1时该命题也成立，现已知当n=9时该命题不成立，那么可推得（　　）
    A．当n=10时，该命题不成立B．当n=10时，该命题成立
    C．当n=8时，该命题成立D．当n=8时，该命题不成立

    查看答案和解析>>

    同步练习册答案