
【题目】如图所示,三棱柱![]() 中,已知
中,已知![]() 侧面
侧面![]() .
.
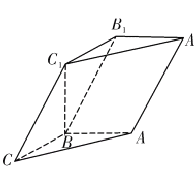
(1)求证: ![]() 平面
平面![]() ;
;
(2)![]() 是棱长
是棱长![]() 上的一点,若二面角
上的一点,若二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)证明AB⊥BC1,在△CBC1中,由余弦定理求解B1C,然后证明BC⊥BC1,利用直线与平面垂直的判定定理证明C1B⊥平面ABC.
(Ⅱ)通过AB,BC,BC1两两垂直.以B为原点,BC,BA,BC1所在直线为x,y,z轴建立空间直角坐标系.求出相关点的坐标,求出平面AB1E的一个法向量,平面的一个法向量通过向量的数量积,推出λ的方程,求解即可.
试题解析: ![]() 证明:因为
证明:因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
由余弦定理得: ![]() ,
,
故![]() ,所以
,所以![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 由
由![]() 可以知道
可以知道![]() ,
, ![]() ,
, ![]() ,两两垂直,以
,两两垂直,以![]() 为原点
为原点![]() ,
, ![]() ,
, ![]() ,所在直线为
,所在直线为![]() ,
, ![]() ,
, ![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
令![]() ,∴
,∴![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
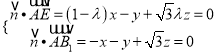 ,
,
令![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
![]() ,两边平方并化简得
,两边平方并化简得![]() ,所以
,所以![]() 或
或![]() .
.
∴![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 满足:①
满足:①![]() ;②所有项
;②所有项![]() ;③
;③ ![]() .
.
设集合![]() ,将集合
,将集合![]() 中的元素的最大值记为
中的元素的最大值记为![]() .换句话说,
.换句话说, ![]() 是
是
数列![]() 中满足不等式
中满足不等式![]() 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列![]() 为数列
为数列![]() 的
的
伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列![]() 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列![]() ;
;
(2)设![]() ,求数列
,求数列![]() 的伴随数列
的伴随数列![]() 的前100之和;
的前100之和;
(3)若数列![]() 的前
的前![]() 项和
项和![]() (其中
(其中![]() 常数),试求数列
常数),试求数列![]() 的伴随数列
的伴随数列![]() 前
前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 是曲线
是曲线![]() 上的一动点,以坐标原点为极点,
上的一动点,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹的极坐标方程;
的轨迹的极坐标方程;
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一矩形硬纸板材料(厚度忽略不计),一边![]() 长为6分米,另一边足够长.现从中截取矩形
长为6分米,另一边足够长.现从中截取矩形![]() (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中
(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中![]() 是以
是以![]() 为圆心、
为圆心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分别与边
分别与边![]() ,
, ![]() 相切于点
相切于点![]() ,
, ![]() .
.
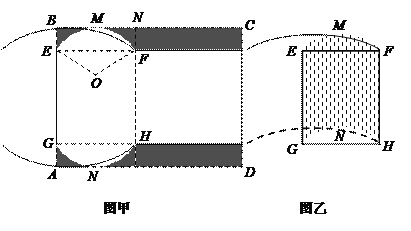
(1)当![]() 长为1分米时,求折卷成的包装盒的容积;
长为1分米时,求折卷成的包装盒的容积;
(2)当![]() 的长是多少分米时,折卷成的包装盒的容积最大?
的长是多少分米时,折卷成的包装盒的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围;
的取值范围;
(2)在(1)中, ![]() 取最小值时,设函数
取最小值时,设函数![]() .若函数
.若函数![]() 在区间
在区间![]() 上恰有两个零点,求实数
上恰有两个零点,求实数![]() 的取值范围;
的取值范围;
(3)证明不等式: ![]() (
(![]() 且
且![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l经过点P(2,0),其倾斜角为,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l与曲线C有公共点,求倾斜角的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①从匀速传递的产品生产流水线上,质检员每30分钟从生产流水线中抽取一件产品进行某项指标检测,这样的抽样方法是系统抽样;
②两个变量的线性相关程度越强,则相关系数的值越接近于1;
③两个分类变量![]() 与
与![]() 的观测值
的观测值![]() ,若
,若![]() 越小,则说明“
越小,则说明“![]() 与
与![]() 有关系”的把握程度越大;
有关系”的把握程度越大;
④随机变量![]() ~
~![]() ,则
,则![]() .
.
其中为真命题的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com