Question

已知奇函数在上有意义，且在上是增函数，

(1)求满足不等式的实数的取值范围；

(2)设函数，若集合，集合 ，求

 

Answer 1

【答案】

(1) x < －1或0 < x < 1     (2) {m | m > 4－2}

【解析】(1) f (－1) = －f (1) = 0，又f (x) 在 (0,+¥) 上是增函数，

∴  f (x) 在 (－¥,0) 上也是增函数，

∴  由 f (x) < 0得x < －1或0 < x < 1.

(2) N = {m | f [g(q)] < 0} = {m | g(q) < －1或0 < g(q) < 1}，

M∩N = {m | g(q) < －1}……………3分

由g(q) < －1得 sin ²q + m cos q－2m < －1 Þ cos ²q－m cos q + 2m－2 > 0 恒成立

 Þ (cos ²q－m cos q + 2m－2)_min > 0

然后换元构造函数设t = cosq，h(t) = cos ²q－m cos q + 2m－2

= t ²－mt + 2m－2 ,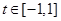求其最值即可

(1)依题意，f (－1) = －f (1) = 0，又f (x) 在 (0,+¥) 上是增函数，

∴  f (x) 在 (－¥,0) 上也是增函数，

∴  由 f (x) < 0得x < －1或0 < x < 1…………… 2分

(2)N = {m | f [g(q)] < 0} = {m | g(q) < －1或0 < g(q) < 1}，

M∩N = {m | g(q) < －1}……………3分

由g(q) < －1得 sin ²q + m cos q－2m < －1 Þ cos ²q－m cos q + 2m－2 > 0 恒成立

 Þ (cos ²q－m cos q + 2m－2)_min > 0…………………4分

设t = cosq，h(t) = cos ²q－m cos q + 2m－2 = t ²－mt + 2m－2

= (t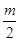－) ²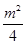－+ 2m－2,

∵  cosq∈[－1,1] Þ t∈[－1,1]，h(t) 的对称轴为 t = 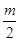…5分

1° 当 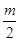> 1，即 m > 2 时，h(t) 在 [－1,1] 为减函数

∴  h(t)_min = h(1) = m－1 > 0 Þ m > 1 Þ m > 2…………………7分

2° 当 －1≤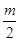≤1，即 －2≤m≤2 时，

∴  h(t)_min = h(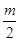) = 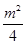－+ 2m－2 > 0 Þ 4－2< m < 4 + 2 

Þ 4－2< m≤2…………9分

3° 当 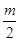< －1，即 m < －2 时，h(t) 在 [－1,1] 为增函数

∴  h(t)_min = h(－1) = 3m－1 > 0 Þ m > 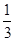无解………………11分

综上，m > 4－2 Þ M∩N = {m | m > 4－2}……………12分

另解：. 解：依题意，f (－1) = －f (1) = 0，又f (x) 在 (0,+¥) 上是增函数，

∴  f (x) 在 (－¥,0) 上也是增函数，

∴  由 f (x) < 0得x < －1或0 < x < 1……………… 2分

∴  N = {m | f [g(q)] < 0} = {m | g(q) < －1或0 < g(q) < 1}，

M∩N = {m | g(q) < －1}…………………3分

由g(q) < －1得 sin ²q + m cos q－2m < －1 Þ cos ²q－m cos q + 2m－2 > 0 恒成立

 Þ (cos ²q－m cos q + 2m－2)_min > 0

设t = cosq，h(t) = cos ²q－m cos q + 2m－2 = t ²－mt + 2m－2 = (t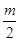－) ²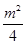－+ 2m－2

∵  cosq∈[－1,1] Þ t∈[－1,1]，h(t) 的对称轴为 t = 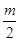，△= m ²－8m + 8 …4分

1° 当 △< 0，即 4－2< m < 4 + 2时，h(t) > 0 恒成立.…………………6分

2° 当 △≥0，即 m≤4－2或 m≥4 + 2时，………7分

由 h(t) > 0 在 [－1,1] 上恒成立

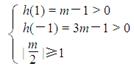∴  Þ m≥2 Þ m≥4 + 2………………11分

综上，m > 4－2 Þ M∩N = {m | m > 4－2}