Question

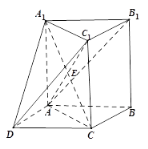
【题目】如图所示的几何体中，为直三棱柱，四边形为平行四边形，，，.

（1）证明：四点共面，且；

（2）若，点是上一点，求四棱锥的体积，并判断点到平面的距离是否为定值？请说明理由.

Answer 1

【答案】（1）证明见解析 （2）到平面的距离为定值，理由见解析

【解析】

（1）利用平行的传递性即可得到四边形为平行四边形，故，，，四点共面.根据已知得到，再利用勾股定理得到，即可证明平面，即.

（2）由（1）知平面，故四棱锥的高为，再计算其体积即可.因为∥，所以点到平面的距离为定值，且等于.

（1）证明：因为为直三棱柱，

所以∥，且，又因为四边形为平行四边形，

所以∥，且，所以∥，且，

所以四边形为平行四边形，所以，，，四点共面.

因为，又平面，

所以，所以四边形为正方形，连接交于，

所以.

在中，，.

由余弦定理得，

所以，所以，

所以，又，

所以平面，所以，

又因为，所以平面；

所以.

（2）解：由（1）知：平面，

在△中，由已知得，所以，

所以四棱锥的体积.

因为∥，所以点到平面的距离为定值，

即为点到平面的距离.