
【题目】已知正项等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() 。数列
。数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。
。
(1)求数列![]() 的通项公式及其前
的通项公式及其前![]() 项和
项和![]() ;
;
(2)证明数列![]() 为等差数列,并求出
为等差数列,并求出![]() 的通项公式;
的通项公式;
(3)设数列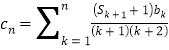 ,问是否存在正整数
,问是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列,若存在,求出所有满足要求的
成等差数列,若存在,求出所有满足要求的![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() ;(3)存在正整数
;(3)存在正整数![]()
![]() ,使得
,使得![]() 成等差数列。理由见解析。
成等差数列。理由见解析。
【解析】
(1)利用等比数列基本量运算即可得到数列![]() 的通项公式及其前
的通项公式及其前![]() 项和
项和![]() ;(2)由
;(2)由![]() 得到
得到![]() ,进而求得
,进而求得![]() ,利用等差数列定义证明即可;(3) 因为
,利用等差数列定义证明即可;(3) 因为![]() ,所以
,所以![]() ,利用反证法即可证明.
,利用反证法即可证明.
(1)设正项等比数列![]() 的公比为
的公比为![]() ,则由
,则由![]() 得
得![]() ,从而
,从而![]() ,又由
,又由![]() 得
得![]() ,因此,
,因此,![]() ,
,
所以![]() ,
,![]() 。
。
(2)方法一:因为![]() ,所以
,所以![]() ,
,
从而数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,故
为公差的等差数列,故![]() ,
,
故![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() 时适合,因此,
时适合,因此,![]() ,
,
从而当![]() 时,
时,![]() 为常数,所以,数列
为常数,所以,数列![]() 为等差数列。
为等差数列。
方法二:因为![]() ,
,
所以,当![]() 时,有
时,有![]() ,
,
两式相减得:![]() ,即
,即![]() ,
,
故![]() ,即
,即![]() ,
,
又由![]() 得
得![]() ,从而
,从而![]() ,故
,故![]() ,
,
所以,数列![]() 为等差数列。
为等差数列。
(3)因为![]() ,
,
所以![]() ,
,
假设存在存在正整数![]()
![]() ,使得
,使得![]() 成等差数列,则
成等差数列,则
![]() ,即
,即![]() ,
,
令![]() ,则原问题等价于存在正整数
,则原问题等价于存在正整数![]() ,使得
,使得![]() ,即
,即![]() 成立。
成立。
因为![]() (因为
(因为![]() ),故数列
),故数列![]() 单调递增,
单调递增,
若![]() ,即
,即![]() ,则
,则![]() ,
,
从而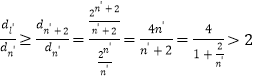 ,即
,即![]() ,而
,而![]() ,
,
因此,![]() ,这与
,这与![]() 恒成立矛盾,故只能有
恒成立矛盾,故只能有![]() ,即
,即![]() ,
,
从而![]() ,故
,故![]() ,即
,即![]() , (*)
, (*)
①若![]() 为奇数,,则记
为奇数,,则记![]() ,从而
,从而![]() ,
,
因为数列![]() 单调递增,所以数列
单调递增,所以数列![]() 单调递减,故当
单调递减,故当![]() 时,
时,![]() ,而
,而![]() ,故
,故![]() ,因此,(*)式无正整数解。
,因此,(*)式无正整数解。
②若![]() 为偶数,则记
为偶数,则记![]() ,即
,即![]() ,同理可得(*)无正整数解。
,同理可得(*)无正整数解。
综上,不存在存在正整数![]() ,使得
,使得![]() 成等差数列,也即不存在正整数
成等差数列,也即不存在正整数![]()
![]() ,使得
,使得![]() 成等差数列。
成等差数列。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60°,G为BC的中点,H为CD中点.
,DE=3,∠BAD=60°,G为BC的中点,H为CD中点.
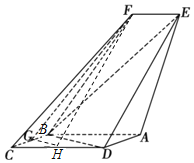
(1)求证:平面FGH∥平面BED;
(2)求证:BD⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园举办雕塑展览吸引着四方宾客,旅游人数![]() 与人均消费
与人均消费![]() (元)的关系如下:
(元)的关系如下: .
.
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入![]() 的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦长为
相交所得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求直线
,若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
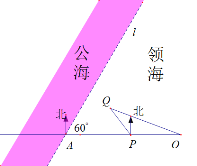
【题目】某海警基地码头![]() 的正西方向
的正西方向![]() 海里处有海礁界碑
海里处有海礁界碑![]() ,过点
,过点![]() 且与
且与![]() 成
成![]() 角(即北偏东
角(即北偏东![]() )的直线
)的直线![]() 为此处的一段领海与公海的分界线(如图所示)。在码头
为此处的一段领海与公海的分界线(如图所示)。在码头![]() 的正西方向且距离
的正西方向且距离![]() 点
点![]() 海里的领海海面
海里的领海海面![]() 处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从
处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从![]() 处即刻出发。若巡逻艇以可疑船的航速的
处即刻出发。若巡逻艇以可疑船的航速的![]() 倍
倍![]() 前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点
前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点![]() 处截获可疑船。
处截获可疑船。
(1)若可疑船的航速为![]() 海里
海里![]() 小时,
小时,![]() ,且可疑船沿北偏西
,且可疑船沿北偏西![]() 的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
(2)若要确保在领海内(包括分界线)成功拦截可疑船,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 四个景点,一位游客来该市游览,已知该游客游览
四个景点,一位游客来该市游览,已知该游客游览![]() 的概率为
的概率为![]() ,游览
,游览![]() 、
、![]() 和
和![]() 的概率都是
的概率都是![]() ,且该游客是否游览这四个景点相互独立.
,且该游客是否游览这四个景点相互独立.
(1)求该游客至多游览一个景点的概率;
(2)用随机变量![]() 表示该游客游览的景点的个数,求
表示该游客游览的景点的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.4万元/分钟和0.2万元分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是()万元
A.72B.80C.84D.90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com