
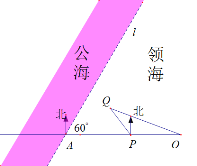
【题目】某海警基地码头![]() 的正西方向
的正西方向![]() 海里处有海礁界碑
海里处有海礁界碑![]() ,过点
,过点![]() 且与
且与![]() 成
成![]() 角(即北偏东
角(即北偏东![]() )的直线
)的直线![]() 为此处的一段领海与公海的分界线(如图所示)。在码头
为此处的一段领海与公海的分界线(如图所示)。在码头![]() 的正西方向且距离
的正西方向且距离![]() 点
点![]() 海里的领海海面
海里的领海海面![]() 处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从
处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从![]() 处即刻出发。若巡逻艇以可疑船的航速的
处即刻出发。若巡逻艇以可疑船的航速的![]() 倍
倍![]() 前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点
前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点![]() 处截获可疑船。
处截获可疑船。
(1)若可疑船的航速为![]() 海里
海里![]() 小时,
小时,![]() ,且可疑船沿北偏西
,且可疑船沿北偏西![]() 的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
(2)若要确保在领海内(包括分界线)成功拦截可疑船,求![]() 的最小值。
的最小值。
【答案】(1)![]() 小时;(2)
小时;(2)![]() 。
。
【解析】
(1) 设![]() ,则
,则![]() ,利用余弦定理求出a值,进而得到巡逻艇成功拦截可疑船所用的时间;
,利用余弦定理求出a值,进而得到巡逻艇成功拦截可疑船所用的时间;
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的平面直角坐标系,则
轴的正方向,建立如图所示的平面直角坐标系,则![]() ,设
,设![]() ,可疑船被截获的轨迹是以
,可疑船被截获的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,利用直线与圆的位置关系得到结果.
为半径的圆,利用直线与圆的位置关系得到结果.
(1)因为巡逻艇的航速是可疑船的航速的2倍,可疑船的航速为![]() 海里/小时,所以巡逻艇的航速为
海里/小时,所以巡逻艇的航速为![]() 海里/小时,且
海里/小时,且![]() ,设
,设![]() ,则
,则![]() ,
,
又可疑船沿北偏西![]() 的方向朝公海逃跑,所以
的方向朝公海逃跑,所以![]() ,
,
在![]() 中,有
中,有![]() ,
,
即![]() ,故
,故![]() ,解得
,解得![]() (负值舍去)
(负值舍去)
所以![]() 小时。
小时。
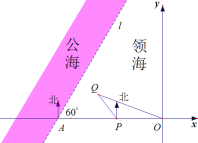
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的平面直角坐标系,则
轴的正方向,建立如图所示的平面直角坐标系,则![]() ,设
,设![]() ,
,
因为巡逻艇的航速是可疑船的航速的![]() 倍,所以
倍,所以![]() ,
,
故![]() ,即
,即![]()
故可疑船被截获的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,
为半径的圆,
又直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
要确保在领海内(包括分界线)成功拦截可疑船,则:
圆心![]() 在直线
在直线![]() 下方,且
下方,且![]() 的轨迹与直线
的轨迹与直线![]() 至多只有一个公共点,
至多只有一个公共点,
所以![]() 且
且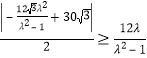
即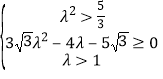 ,解得
,解得![]() ,
,
故要确保在领海内(包括分界线)成功拦截可疑船,则![]() 。
。


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
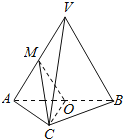
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
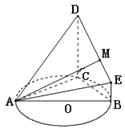
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的是( )
A.半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B.直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.用一个平面截圆锥底面与截面组成的部分是圆台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若A、B、C、D是空间任意四点,则有![]() ;
;
②![]() 是
是![]() 、
、![]() 共线的充要条件;
共线的充要条件;
③对空间任意一点P与不共线的三点A、B、C,若![]() ,(
,(![]() ,y,z∈R),则P、A、B、C四点共面.
,y,z∈R),则P、A、B、C四点共面.
其中不正确命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() 。数列
。数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。
。
(1)求数列![]() 的通项公式及其前
的通项公式及其前![]() 项和
项和![]() ;
;
(2)证明数列![]() 为等差数列,并求出
为等差数列,并求出![]() 的通项公式;
的通项公式;
(3)设数列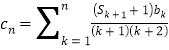 ,问是否存在正整数
,问是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列,若存在,求出所有满足要求的
成等差数列,若存在,求出所有满足要求的![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点P是直线2x+y+10=0上的动点,直线PA、PB分别与圆x2+y2=4相切于A、B两点,则四边形PAOB(O为坐标原点)面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
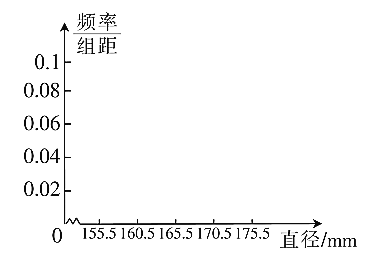
【题目】(1)从某厂生产的一批零件1000个中抽取20个进行研究,应采用什么抽样方法?
(2)对(1)中的20个零件的直径进行测量,得到下列不完整的频率分布表:(单位:mm)
分组 | 频数 | 频率 |
| 2 | |
| 6 | |
| 8 | |
| ||
合计 | 20 | 1 |
①完成频率分布表;
②画出其频率分布直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com