
ΓΨΧβΡΩΓΩΓΨ2017’ρΫ≠“ΜΡΘΓΩ»γΆΦΘ§Ρ≥ΙΪ‘Α”–»ΐΧθΙέΙβ¥σΒά![]() Έß≥…÷±Ϋ«»ΐΫ«–ΈΘ§Τδ÷–÷±Ϋ«±Ώ
Έß≥…÷±Ϋ«»ΐΫ«–ΈΘ§Τδ÷–÷±Ϋ«±Ώ![]() Θ§
Θ§
–±±Ώ![]() Θ°œ÷”–ΦΉΓΔ““ΓΔ±ϊ»ΐΈΜ–Γ≈σ”―Ζ÷±π‘Ύ
Θ°œ÷”–ΦΉΓΔ““ΓΔ±ϊ»ΐΈΜ–Γ≈σ”―Ζ÷±π‘Ύ![]() ¥σΒά…œφ“œΖΘ§Υυ‘ΎΈΜ
¥σΒά…œφ“œΖΘ§Υυ‘ΎΈΜ
÷ΟΖ÷±πΦ«ΈΣΒψ![]() Θ°
Θ°
Θ®1Θ©»τΦΉ““ΕΦ“‘ΟΩΖ÷÷”![]() ΒΡΥΌΕ»¥”Βψ
ΒΡΥΌΕ»¥”Βψ![]() ≥ωΖΔ‘ΎΗςΉ‘ΒΡ¥σΒά…œ±ΦΉΏΘ§ΒΫ¥σΒάΒΡΝμ“ΜΕΥ
≥ωΖΔ‘ΎΗςΉ‘ΒΡ¥σΒά…œ±ΦΉΏΘ§ΒΫ¥σΒάΒΡΝμ“ΜΕΥ
±Φ¥ΆΘΘ§““±»ΦΉ≥Ό![]() Ζ÷÷”≥ωΖΔΘ§Β±““≥ωΖΔ
Ζ÷÷”≥ωΖΔΘ§Β±““≥ωΖΔ![]() Ζ÷÷”ΚσΘ§«σ¥Υ ±ΦΉ““ΝΫ»Υ÷°ΦδΒΡΨύάκΘΜ
Ζ÷÷”ΚσΘ§«σ¥Υ ±ΦΉ““ΝΫ»Υ÷°ΦδΒΡΨύάκΘΜ
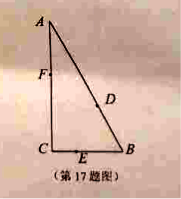
Θ®2Θ©…η![]() Θ§““±ϊ÷°ΦδΒΡΨύάκ «ΦΉ““÷°ΦδΨύάκΒΡ
Θ§““±ϊ÷°ΦδΒΡΨύάκ «ΦΉ““÷°ΦδΨύάκΒΡ![]() ±ΕΘ§«“
±ΕΘ§«“![]() Θ§«κΫΪΦΉ
Θ§«κΫΪΦΉ
““÷°ΦδΒΡΨύάκ![]() ±μ ΨΈΣ
±μ ΨΈΣ![]() ΒΡΚ· ΐΘ§≤Δ«σΦΉ““÷°ΦδΒΡΉν–ΓΨύάκΘ°
ΒΡΚ· ΐΘ§≤Δ«σΦΉ““÷°ΦδΒΡΉν–ΓΨύάκΘ°
 ΧΊΗΏΦΕΫΧ ΠΒψ≤ΠœΒΝ–¥πΑΗ
ΧΊΗΏΦΕΫΧ ΠΒψ≤ΠœΒΝ–¥πΑΗ ΈΡΨ¥ΆΦ ιΩΈ ±œ»ΖφœΒΝ–¥πΑΗ
ΈΡΨ¥ΆΦ ιΩΈ ±œ»ΖφœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΨ2017ΚΰΡœ≥Λ…≥ΕΰΡΘΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() .
.
Θ®1Θ©÷ΛΟςΘΚ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΕΦ≤Μ ««ζœΏ
ΕΦ≤Μ ««ζœΏ![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©»τ![]() Θ§ Ι
Θ§ Ι![]() ≥…ΝΔΘ§«σ Β ΐ
≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ“Μ»ΐΫ«–Έ»ΐ±ΏΥυ‘ΎΒΡ÷±œΏΖΫ≥ΧΖ÷±πΈΣx+2y©¹5=0Θ§y©¹2=0Θ§x+y©¹4=0Θ§‘ρΡήΙΜΗ≤Η«¥Υ»ΐΫ«–Έ«“ΟφΜΐΉν–ΓΒΡ‘≤ΒΡΖΫ≥ΧΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ’ΐΖΫΧεABCD©¹A1B1C1D1÷–Θ§Ε·ΒψP‘ΎΒΉΟφABCDΡΎΘ§«“PΒΫάβADΒΡΨύάκ”κΒΫΟφΕ‘Ϋ«œΏBC1ΒΡΨύάκœύΒ»Θ§‘ρΒψPΒΡΙλΦΘ «Θ®ΓΓΓΓΘ©
A.œΏΕΈ
B.Ά÷‘≤ΒΡ“Μ≤ΩΖ÷
C.ΥΪ«ζœΏΒΡ“Μ≤ΩΖ÷
D.≈ΉΈοœΏΒΡ“Μ≤ΩΖ÷
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΨΥ’±±ΥΡ –2016-2017―ßΡξΕ»ΗΏ»ΐΡξΦΕΒΎ“Μ―ßΤΎΤΎΡ©Βς―–ΓΩ»γΆΦΘ§“―÷Σ![]() ΝΫ’ρΖ÷±πΈΜ”ΎΕΪΈςΚΰΑΕ
ΝΫ’ρΖ÷±πΈΜ”ΎΕΪΈςΚΰΑΕ![]() ΒΡ
ΒΡ![]() ¥ΠΚΆΚΰ÷––ΓΒΚΒΡ
¥ΠΚΆΚΰ÷––ΓΒΚΒΡ![]() ¥ΠΘ§Βψ
¥ΠΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ
ΒΡ
’ΐΈςΖΫœρ![]() ¥ΠΘ§
¥ΠΘ§![]() Θ°œ÷ΦΤΜ°ΤΧ…η“ΜΧθΒγά¬ΝΣΆ®
Θ°œ÷ΦΤΜ°ΤΧ…η“ΜΧθΒγά¬ΝΣΆ®![]() ΝΫ’ρΘ§”–
ΝΫ’ρΘ§”–
ΝΫ÷÷ΤΧ…ηΖΫΑΗΘΚΔΌ―ΊœΏΕΈ![]() ‘ΎΥ°œ¬ΤΧ…ηΘΜΔΎ‘ΎΚΰΑΕ
‘ΎΥ°œ¬ΤΧ…ηΘΜΔΎ‘ΎΚΰΑΕ![]() …œ―Γ“ΜΒψ
…œ―Γ“ΜΒψ![]() Θ§œ»―ΊœΏΕΈ
Θ§œ»―ΊœΏΕΈ![]() ‘ΎΒΊ
‘ΎΒΊ
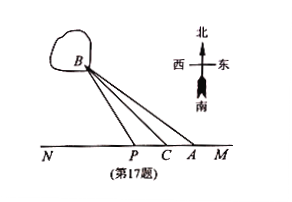
œ¬ΤΧ…ηΘ§‘Ό―ΊœΏΕΈ![]() ‘ΎΥ°œ¬ΤΧ…ηΘ§‘ΛΥψΒΊœ¬ΓΔΥ°œ¬ΒΡΒγά¬ΤΧ…ηΖ―”ΟΖ÷±πΈΣ
‘ΎΥ°œ¬ΤΧ…ηΘ§‘ΛΥψΒΊœ¬ΓΔΥ°œ¬ΒΡΒγά¬ΤΧ…ηΖ―”ΟΖ÷±πΈΣ![]() Άρ‘Σ®M
Άρ‘Σ®M![]() ΓΔ
ΓΔ
![]() Άρ‘Σ®M
Άρ‘Σ®M![]() Θ°
Θ°
Θ®1Θ©«σ![]() ΝΫ’ρΦδΒΡΨύάκΘΜ
ΝΫ’ρΦδΒΡΨύάκΘΜ
Θ®2Θ©”ΠΗΟ»γΚΈΤΧ…ηΘ§ ΙΉήΤΧ…ηΖ―”ΟΉνΒΆΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΨ2017Ν…ΡΰΚυ¬ΪΒΚ –ΕΰΡΘΓΩ“―÷Σ ΐΝ–![]() ¬ζΉψΘΚ
¬ζΉψΘΚ ![]() .
.
Θ®1Θ©«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©»τ![]() ,«σ ΐΝ–
,«σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆ
œνΚΆ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η ΐΝ–{an}ΒΡ«ΑœνΚΆΈΣSn Θ§ «“Sn= ![]() Θ§{bn}ΈΣΒ»≤ν ΐΝ–Θ§«“a1=b1 Θ§ a2Θ®b2©¹b1Θ©=a1 Θ°
Θ§{bn}ΈΣΒ»≤ν ΐΝ–Θ§«“a1=b1 Θ§ a2Θ®b2©¹b1Θ©=a1 Θ°
Θ®1Θ©«σ ΐΝ–{an}ΚΆ{bn}Ά®œνΙΪ ΫΘΜ
Θ®2Θ©…η ![]() Θ§«σ ΐΝ–{cn}ΒΡ«ΑnœνΚΆTn Θ°
Θ§«σ ΐΝ–{cn}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§Ϋ«AΓΔBΓΔCΥυΕ‘ΒΡ±ΏΖ÷±π «aΓΔbΓΔcΘ§«“¬ζΉψcsinA©¹ ![]() acosC=0Θ°
acosC=0Θ°
Θ®1Θ©«σΫ«CΒΡ¥σ–ΓΘΜ
Θ®2Θ©»τc=2Θ§«σΓςABCΒΡΟφΜΐSΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΨ2017Α≤Μ’Μ¥±±ΕΰΡΘΓΩ―Γ–ό4ΓΣ4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–, “‘
÷–, “‘![]() ΈΣΦΪΒψ,
ΈΣΦΪΒψ, ![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒ, ‘≤
÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒ, ‘≤![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() ,÷±œΏ
,÷±œΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ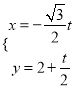 Θ®tΈΣ≤Έ ΐΘ©Θ§ ÷±œΏ
Θ®tΈΣ≤Έ ΐΘ©Θ§ ÷±œΏ![]() ΚΆ‘≤
ΚΆ‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΓΘ
ΝΫΒψΓΘ
Θ®ΔώΘ©«σ‘≤–ΡΒΡΦΪΉχ±ξΘΜ
Θ®ΔρΘ©÷±œΏ![]() ”κ
”κ![]() ÷αΒΡΫΜΒψΈΣ
÷αΒΡΫΜΒψΈΣ![]() Θ§«σ
Θ§«σ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com