
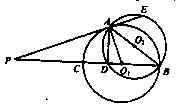
如图, 相交于A、B两点,AB是
相交于A、B两点,AB是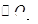 的直径,过A点作
的直径,过A点作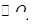 的切线交
的切线交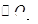 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与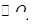 、
、 交于C,D两点.
交于C,D两点.
求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE.
科目:高中数学 来源: 题型:
 椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:| x | 3 |
|
4 |
| ||||||
| y | -
|
|
-2 |
|
| AM |
| 1 |
| 2 |
| MB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=
如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
(2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
|
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:2010年上海市高一第二学期阶段质量检测数学试题 题型:填空题
如图,半径为1的圆与直线l相交于A、B两个不同的点,设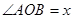 ,当直
,当直
线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积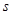 关于
关于 的函数
的函数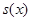 =____________________.
=____________________.
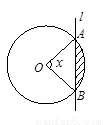
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
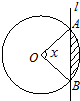 如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=________.
如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com