已知圆E经过点A(2,-3)、B(-2,-5),且圆心在直线x-2y-3=0上.
(1)求圆E的方程;
(2)若直线x+y+m=0与圆E交于P、Q两点,且 EP⊥EQ,求m的值.
【答案】
分析:(1)根据圆心E在直线x-2y-3=0,可设圆心E( 2b+3,b ),由|EA|=|EB|列出方程解出 b=-2,求得圆心E的坐标即半径,从而得到圆的标准方程.
(2)设圆心到直线的距离为d,由题意可得
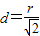
,即
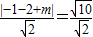
,解此方程求出m的值.
解答:解:(1)∵圆心E在直线x-2y-3=0,可设圆心E(2b+3,b ).
由|EA|=|EB|可得
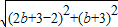
=
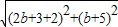
,
平方化简可得 5b
2+10b+10=5b
2+30b+30,
解得 b=-2,故点E(-1,-2).
由两点间距离公式得r
2 =|EA|
2=10,
所以,圆的方程为(x+1)
2+(y+2)
2=10.
(2)由题意可得△EPQ为等腰直角三角形,EP=EQ=r=
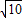
,
设圆心到直线PQ的距离为d,可得
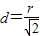
,
再由点E(-1,-2),PQ的方程为x+y+m=0,故有
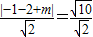
,
解得
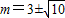
.
点评:本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键.直线和圆的位置关系,点到直线的距离公式的应用,属于中档题.

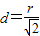 ,即
,即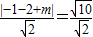 ,解此方程求出m的值.
,解此方程求出m的值.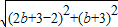 =
=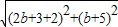 ,
,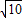 ,
,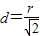 ,
,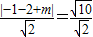 ,
,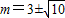 .
.

 (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲]