
【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,离心率
,离心率![]() ,其中一个焦点的坐标为
,其中一个焦点的坐标为![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当点![]() 在椭圆
在椭圆![]() 上运动时,设动点
上运动时,设动点![]() 的运动轨迹为
的运动轨迹为![]() 若点
若点![]() 满足:
满足: ![]() 其中
其中![]() 是
是![]() 上的点.直线
上的点.直线![]() 的斜率之积为
的斜率之积为![]() ,试说明:是否存在两个定点
,试说明:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ) ![]() (Ⅱ)详见解析.
(Ⅱ)详见解析.
【解析】试题分析: (Ⅰ)根据离心率和焦点坐标以及![]() 求出椭圆的标准方程;(Ⅱ)由于点
求出椭圆的标准方程;(Ⅱ)由于点![]() 在曲线
在曲线![]() 上运动时,动点
上运动时,动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ,通过
,通过![]() 可建立点T和点M,N坐标之间的关系式,通过直线
可建立点T和点M,N坐标之间的关系式,通过直线![]() 的斜率之积为定值,又得到另外一个关系式,且点M,N的坐标满足椭圆的方程,均为二次,因此给两等式分别平方,再对应系数比为1:2,相加即可得到关于x,y的方程,即点T的轨迹为椭圆,两个定点为焦点.
的斜率之积为定值,又得到另外一个关系式,且点M,N的坐标满足椭圆的方程,均为二次,因此给两等式分别平方,再对应系数比为1:2,相加即可得到关于x,y的方程,即点T的轨迹为椭圆,两个定点为焦点.
试题解析:(Ⅰ)由题意知, ![]() 所以
所以![]() 所以
所以![]()
故椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设![]() 则
则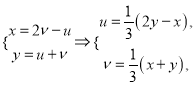
因为点![]() 在椭圆
在椭圆![]() 上运动,所以
上运动,所以![]()
故动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
由![]() 得
得
![]()
![]()
设![]() 分别为直线
分别为直线![]() 的斜率,由已知条件知
的斜率,由已知条件知![]() ,所以
,所以![]()
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]()
故![]()
![]()
从而知![]() 点是椭圆
点是椭圆![]() 上的点,所以,存在两个定点
上的点,所以,存在两个定点![]() 且为椭圆
且为椭圆![]() 的两个焦点,使得
的两个焦点,使得![]() 为定值.其坐标分别为
为定值.其坐标分别为![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() :
:![]() (
(![]() )分别交
)分别交![]() ,
,![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
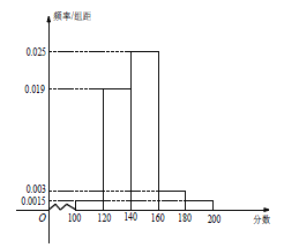
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中曲线
中曲线![]() 经伸缩变换
经伸缩变换![]() 后得到曲线
后得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一点,又
上的一点,又![]() 向曲线
向曲线![]() 引切线,切点为
引切线,切点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于
名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于![]() 分者为“成绩优良”.
分者为“成绩优良”.

(1)分别计算甲、乙两班![]() 个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率;
人来自不同班级的概率;
(3)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: 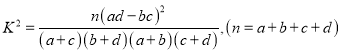
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)已知的椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,上顶点
,上顶点![]() ,
, ![]() 是正三角形且周长为6.
是正三角形且周长为6.
(1)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(2) ![]() 为坐标原点,
为坐标原点, ![]() 是直线
是直线![]() 上的一个动点,求
上的一个动点,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com