
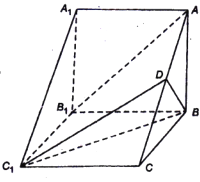
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)3
【解析】试题分析:(1)欲证![]() 平面
平面![]() ,根据线面平行的判定定理可知只需证
,根据线面平行的判定定理可知只需证![]() 与平面
与平面![]() 内一直线平行,连接
内一直线平行,连接![]() ,设
,设![]() 与
与![]() 相交于点O,连接
相交于点O,连接![]() ,根据中位线定理可知
,根据中位线定理可知![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,满足定理所需条件;
,满足定理所需条件;
(2)根据面面垂直的判定定理可知平面![]() ⊥平面
⊥平面![]() ,作
,作![]() ,垂足为E,则
,垂足为E,则![]() ⊥平面
⊥平面![]() ,然后求出棱长,最后根据四棱锥
,然后求出棱长,最后根据四棱锥![]() ,的体积
,的体积![]() ,即可求四棱锥
,即可求四棱锥![]() 的体积.
的体积.
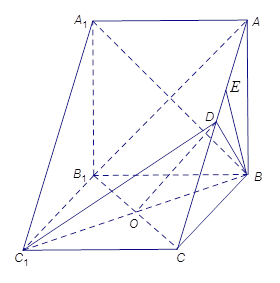
(1)证明:连接![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴点![]() 为
为![]() 的中点.
的中点.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 为△
为△![]() 的中位线,
的中位线,
∴![]() .
.
∵![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴ 平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]()
![]() .
.
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() ,
,
∵![]() ,
,![]() ,
,
在Rt△![]() 中,
中,![]() ,
,![]() ,
,
∴四棱锥![]() 的体积
的体积![]()
![]()
![]() .
.
∴四棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】中国政府实施“互联网+”战略以来,手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式,“一机在手,走遍天下”的时代已经到来。在某著名的夜市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“市场购物用手机支付与年龄有关”?
的把握认为“市场购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件
为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
|
|
|
|
|
|
|
|
|
|
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 24 | ||
合计 | 100 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.

(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,曲线
,曲线![]() 上任意一点
上任意一点![]() 满足;直线
满足;直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过![]() 且斜率为正数的直线
且斜率为正数的直线![]() 与抛物线交于
与抛物线交于![]() 两点,其中点
两点,其中点![]() 在
在![]() 轴上方,与曲线
轴上方,与曲线![]() 交于点
交于点![]() ,若
,若![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,当时
,当时![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,若
,若![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在抛物线
在抛物线![]() 上,是否存在直线
上,是否存在直线![]() 与椭圆交于
与椭圆交于![]() ,使得
,使得![]() 的中点
的中点![]() 落在直线
落在直线![]() 上,并且与抛物线
上,并且与抛物线![]() 相切,若直线
相切,若直线![]() 存在,求出
存在,求出![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数![]() 的图象与
的图象与![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的值;
的值;
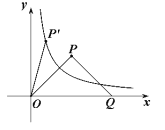
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() ,得到
,得到![]() ,若点
,若点![]() 恰好落在曲线
恰好落在曲线![]() (
(![]() )上(如图所示),试判断点
)上(如图所示),试判断点![]() 是否也落在曲线
是否也落在曲线![]() (
(![]() )上,并说明理由.
)上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
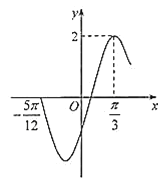
【题目】若函数f(x)=Asin(x+φ)(A>0, ![]() 的部分图象如图所示.
的部分图象如图所示.
(I)设x∈(0, ![]() )且f(α)=
)且f(α)=![]() ,求sin 2a的值;
,求sin 2a的值;
(II)若x∈[![]() ]且g(x)=2λf(x)+cos(4x﹣
]且g(x)=2λf(x)+cos(4x﹣![]() )的最大值为
)的最大值为![]() ,求实数λ的值.
,求实数λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com