
【题目】已知函数![]() (
(![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数![]() 的图象与
的图象与![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
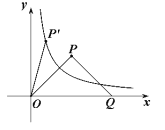
(1)求![]() 的值;
的值;
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() ,得到
,得到![]() ,若点
,若点![]() 恰好落在曲线
恰好落在曲线![]() (
(![]() )上(如图所示),试判断点
)上(如图所示),试判断点![]() 是否也落在曲线
是否也落在曲线![]() (
(![]() )上,并说明理由.
)上,并说明理由.
【答案】(1)2;(2)见解析.
【解析】试题分析:(1)由已知利用周期公式可求最小正周期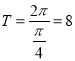 ,由题意可求Q坐标为(4,0).P坐标为(2,
,由题意可求Q坐标为(4,0).P坐标为(2, ![]() ),结合△OPQ为等腰直角三角形,即可得解
),结合△OPQ为等腰直角三角形,即可得解![]() ;
;
(2)由(Ⅰ)知, ![]() ,
, ![]() ,可求点P′,Q′的坐标,由点
,可求点P′,Q′的坐标,由点![]() 在曲线
在曲线![]() ,(x>0)上,利用倍角公式,诱导公式可求
,(x>0)上,利用倍角公式,诱导公式可求![]() ,又结合
,又结合![]() ,,可求
,,可求![]() 的值,由于
的值,由于![]() ,即可证明点Q′不落在曲线
,即可证明点Q′不落在曲线![]() (
(![]() )上.
)上.
试题解析:
(1)因为函数![]() (
(![]() )的最小正周期
)的最小正周期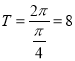 ,所以函数
,所以函数![]() 的半周期为
的半周期为![]() ,
,
所以![]() ,即有
,即有![]() 坐标为
坐标为![]() ,
,
又因为![]() 为函数
为函数![]() 图象的最高点,所以点
图象的最高点,所以点![]() 的坐标为
的坐标为![]() .
.
又因为![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
(2)点![]() 不落在曲线
不落在曲线![]() (
(![]() )上,理由如下:
)上,理由如下:
由(1)知, ![]() ,
, ![]()
所以点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
因为点![]() 在曲线
在曲线![]() (
(![]() )上,所以
)上,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
又![]() .所以点
.所以点![]() 不落在曲线
不落在曲线![]() (
(![]() )上.
)上.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,离心率
,离心率![]() ,
, ![]() 为坐标原点,圆
为坐标原点,圆![]() 与直线
与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知四边形![]() 内接于椭圆
内接于椭圆![]() .记直线
.记直线![]() 的斜率分别为
的斜率分别为![]() ,试问
,试问![]() 是否为定值?证明你的结论.
是否为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技发展,手机成了人们日常生活中必不可少的通信工具,现在的中学生几乎都拥有了属于自己的手机了.为了调查某地区高中生一周使用手机的频率,某机构随机调查了该地区100名高中生某一周使用手机的时间(单位:小时),所取样本数据分组区间为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由此得到如图所示的频率分布直方图.
,由此得到如图所示的频率分布直方图.

(1)求![]() 的值并估计该地区高中生一周使用手机时间的平均值;
的值并估计该地区高中生一周使用手机时间的平均值;
(2)从使用手机时间在![]() 、
、![]() 、
、![]() 、
、![]() 的四组学生中,用分层抽样方法抽取13人,则每层各应抽取多少人?
的四组学生中,用分层抽样方法抽取13人,则每层各应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin 2x-cos2x-
sin 2x-cos2x-![]() ,x∈R.
,x∈R.
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c=![]() ,f(C)=0,若sin B=2sin A,求a,b的值.
,f(C)=0,若sin B=2sin A,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是
(m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)设![]() (其中
(其中![]() 为f (x)的导函数),证明:对任意x > 0,都有
为f (x)的导函数),证明:对任意x > 0,都有![]() .
.
(注: ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com