练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下面几种推理是演绎推理的个数是（ ）

    ①两条直线平行，同旁内角互补。如果∠A与∠B是两条平行直线的同旁内角,那么∠A+∠B=180°；

    ②猜想数列1，3，5，7，9，11，…的通项公式为；

    ③由正三角形的性质得出正四面体的性质；

    ④半径为的圆的面积，则单位圆的面积．

    A. 1个B. 2个C. 3个D. 4个

    【答案】B

    【解析】

    演绎推理是由普通性的前提推出特殊性结论的推理．其形式在高中阶段主要学习了三段论：大前提、小前提、结论，由此对四个命题进行判断得出正确选项．

    解：对于①是演绎推理，大前提是“两条直线平行，同旁内角互补，”，小前提是“∠A与∠B是两条平行直线的同旁内角”，结论是“∠A+∠B＝180°”；

    对于②是由特殊到一般，是归纳推理；

    对于③“正三角形的性质得出正四面体的性质”是类比推理；

    对于④是演绎推理，大前提是“半径为的圆的面积”，小前提是“单位圆”，结论是“单位圆的面积”；

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）讨论函数的单调性；

    （2）若函数在时恒成立，求实数的取值范围；

    （3）若函数，求证：函数的极大值小于1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位现需要将“先进个人”，“业务精英”、“道德模范”、“新长征突击手”、“年度优秀员工”5种荣誉分配给3个人，且每个人至少获得一种荣誉，五种荣誉中“道德模范”与“新长征突击手”不能分给同一个人，则不同的分配方法共有（ ）

    A. 120种 B. 150种 C. 114种 D. 118种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【选修4-4，坐标系与参数方程】

    在直角坐标系中，直线的参数方程为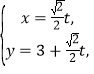（t为参数），在以O为极点，轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为

    （Ⅰ）求直线的普通方程与曲线C的直角坐标方程；

    （Ⅱ）若直线与轴的交点为P，直线与曲线C的交点为A,B,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥，底面为菱形，，,平面，分别是的中点。

    （1）证明：；

    （2）若为上的动点，与平面所成最大角的正切值为，求二面角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中，错误的是（ ）

    A. 若命题，，则命题，

    B. “”是“”的必要不充分条件

    C. “若，则、中至少有一个不小于”的逆否命题是真命题

    D. ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且过点．

    （1）求的方程；

    （2）是否存在直线与相交于两点，且满足：①与（为坐标原点）的斜率之和为2；②直线与圆相切，若存在，求出的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

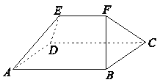
    【题目】我国古代数学名著《九章算术》中记载的“刍甍”（chu meng）是指底面为矩形，顶部只有一条棱的五面体．如图，五面体是一个刍甍，其中是正三角形，，则以下两个结论：①；②，（ ）

    A.①和②都不成立B.①成立，但②不成立

    C.①不成立，但②成立D.①和②都成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x），若存在x0∈R，使f（x0）=x0，则称x0是f（x）的一个不动点，已知f（x）=x2+ax+4在[1，3]恒有两个不同的不动点，则实数a的取值范围______.

    查看答案和解析>>

    同步练习册答案