
【题目】已知函数![]() ,
,![]() .
.
(1)证明:![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(2)若存在![]() ,使得
,使得![]() 与
与![]() 在
在![]() 的值域相同,求实数
的值域相同,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出![]() ,可证明
,可证明![]() ,
,![]() 恒成立,故可得
恒成立,故可得![]() 为
为![]() 上的增函数.
上的增函数.
(2)先讨论![]() 时的情形,此时可把
时的情形,此时可把![]() 的存在性问题转化为
的存在性问题转化为![]() 在
在![]() 存在两个不同的零点问题,利用导数和零点存在定理可得
存在两个不同的零点问题,利用导数和零点存在定理可得![]() .再讨论
.再讨论![]() 的情形,利用两个函数的函数值的符号可判定这种情况不成立,两者结合可求
的情形,利用两个函数的函数值的符号可判定这种情况不成立,两者结合可求![]() 的取值范围.
的取值范围.
(1)因为![]() ,故
,故![]() 且
且![]() ,
,
令![]() ,故
,故![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,
,
故![]() ,
,![]() ,故
,故![]() 为
为![]() 上的增函数.
上的增函数.
(2)因为![]() ,故
,故![]() 在
在![]() 为增函数,
为增函数,
故![]() 在
在![]() 上的值域为
上的值域为![]() .
.
当![]() 时,
时,![]() 的值域为
的值域为![]() ,故
,故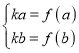 ,
,
所以![]() 在
在![]() 有两个不同的解
有两个不同的解![]() .
.
令![]() ,
,
故![]() 在
在![]() 有两个不同的零点.
有两个不同的零点.
又![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 为
为![]() 上的单调增函数,
上的单调增函数,
故![]() 在
在![]() 最多有一个解,舍去.
最多有一个解,舍去.
当![]() 时,
时,![]() .
.
取![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
故![]() 在
在![]() 为增函数,
为增函数,
故![]() ,
,
故![]() 在
在![]() 有且只有一个实数解
有且只有一个实数解![]() 且
且![]() .
.
当![]() ,
,![]() ,故
,故![]() 在
在![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 为增函数;
为增函数;
故![]() .
.
又![]() ,所以
,所以![]()
因为![]() 在
在![]() 有两个不同的零点,
有两个不同的零点,
故![]() 即
即![]() .
.
令![]() ,其中
,其中![]() ,
,
故![]() ,故
,故![]() 在
在![]() 上为减函数,
上为减函数,
故不等式![]() 的解为
的解为![]() ,
,
所以![]() .
.
令![]() 及
及![]() ,
,
因为![]() 为开口向上的二次函数,
为开口向上的二次函数,
故存在![]() ,使得当任意
,使得当任意![]() 时,总有
时,总有![]() ,
,
而![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
当对任意的![]() 时,总有
时,总有![]() ,
,
因为![]() ,故当
,故当![]() ,
,![]() ,
,
根据零点存在定理,![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
因为![]() 在
在![]() 有两个不同的零点,故
有两个不同的零点,故![]() ,
,
所以![]() 即
即![]() ,
,
又![]() ,故
,故![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() 在
在![]() 上始终满足
上始终满足![]() ,
,
由(1)可知![]() 在
在![]() 为增函数,故
为增函数,故![]() ,
,
不符合题设要求,舍去.
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
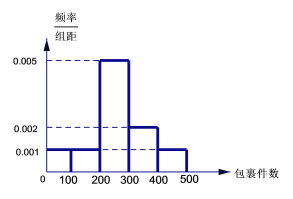
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是
的大小是![]() .连接
.连接![]() ,
,![]() ,如图:
,如图:
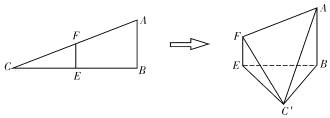
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,有下列三个命题:
翻折过程中,有下列三个命题:
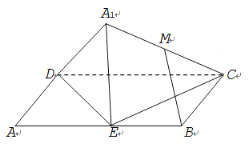
①线段![]() 的长是定值;
的长是定值;
②存在某个位置,使![]() ;
;
③存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题有______. (填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1—13分别对应2017年1月—2018年1月)
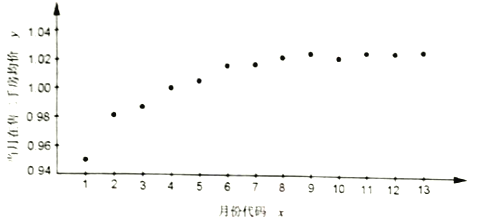
由散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程分别为
两个模型进行拟合,经过数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2018年6月份购买这个小区![]() 平方米的二手房(欲
平方米的二手房(欲
购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2年但未满5年,请你利用(1)中拟合效果更好的模型估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.001万元/平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格进行征收.(计税价格=房款),征收方式见下表:
契税 (买方缴纳) | 首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且144平方米以内(含144平方米)为1.5%;面积144平方米以上或非首套为3% |
增值税 (卖方缴纳) | 房产证未满2年或满2年且面积在144平方米以上(不含144平方米)为5.6%;其他情况免征 |
个人所得税 (卖方缴纳) | 首套面积144平方米以内(含144平方米)为1%;面积144平方米以上或非首套均为1.5%;房产证满5年且是家庭唯一住房的免征 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 参考公式:相关指数
. 参考公式:相关指数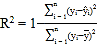 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com