
【题目】(12分)
如图,在四棱锥![]()
![]() .
.
(1)当PB=2时,证明:平面![]() 平面ABCD.
平面ABCD.
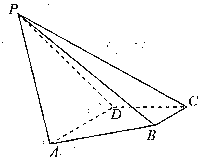 (2)当四棱锥
(2)当四棱锥![]() 的体积为
的体积为![]() ,且二面角
,且二面角![]() 为钝角时,求直线PA与平面PCD所成角的正弦值.
为钝角时,求直线PA与平面PCD所成角的正弦值.
【答案】(1)见解析.
(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,由
,由![]() ,推出
,推出![]() ∥
∥![]() ,根据
,根据![]() ,推出
,推出![]() ,即可证明
,即可证明![]() 为矩形,则
为矩形,则![]() ,即可证明
,即可证明![]() ,从而可证平面
,从而可证平面![]() 平面
平面![]() ;(2)由
;(2)由![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ,可得平面
,可得平面![]()
![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 平面
平面![]() ,根据四棱锥
,根据四棱锥![]() 的体积为
的体积为![]() ,即可算出
,即可算出![]() ,从而可得
,从而可得![]() 的值,以
的值,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴,在平面
轴,在平面![]() 内过点
内过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,分别求出向量
轴,建立空间直角坐标系,分别求出向量![]() 与平面
与平面![]() 的一个法向量,即可求出求直线
的一个法向量,即可求出求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)证明:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
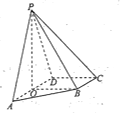
∵![]() 为正三角形
为正三角形
∴![]() .
.
∵![]()
∴![]()
∵![]()
∴![]() ,
,
∴四边形![]() 为矩形
为矩形
∴![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,则
,则![]() .
.
∵![]()
∴![]() 平面
平面![]()
又∵![]() 平面
平面![]()
∴平面![]() 平面
平面![]() .
.
(2)解:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
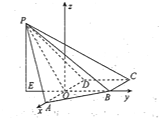
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,所以过点
,所以过点![]() 作
作![]()
![]() 平面
平面![]() ,垂足
,垂足![]() 一定落在平面
一定落在平面![]() 与平面
与平面![]() 的交线
的交线![]() 上.
上.
∵四棱锥![]() 的体积为
的体积为![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
∵![]()
∴![]()
以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴,在平面
轴,在平面![]() 内过点
内过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .由题意可知
.由题意可知![]()
![]() ,故
,故
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则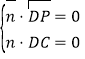 ,即
,即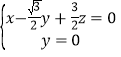 ,令
,令![]() ,则
,则![]() ,所以
,所以![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则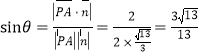 .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是:( )
①设函数![]() 可导,则
可导,则![]() ;
;
②过曲线![]() 外一定点做该曲线的切线有且只有一条;
外一定点做该曲线的切线有且只有一条;
③已知做匀加速运动的物体的运动方程是![]() 米,则该物体在时刻
米,则该物体在时刻![]() 秒的瞬时速度是
秒的瞬时速度是![]() 米
米![]() 秒;
秒;
④一物体以速度![]() (米/秒)做直线运动,则它在
(米/秒)做直线运动,则它在![]() 到
到![]() 秒时间段内的位移为
秒时间段内的位移为![]() 米;
米;
⑤已知可导函数![]() ,对于任意
,对于任意![]() 时,
时,![]() 是函数
是函数![]() 在
在![]() 上单调递增的充要条件.
上单调递增的充要条件.
A. ①③B. ③④C. ②③⑤D. ③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
一只药用昆虫的产卵数y(单位:个)与一定范围内的温度![]() (单位:℃)有关,现收集了该种药用昆虫的6组观测数据如下表所示.
(单位:℃)有关,现收集了该种药用昆虫的6组观测数据如下表所示.

经计算得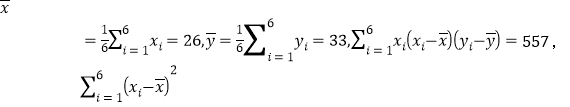
![]()
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]()
![]() ,其中
,其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求![]() 的回归方程
的回归方程![]() (结果精确到0.1).
(结果精确到0.1).
(2)若用非线性回归模型预测当温度为35℃时,该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若命题![]() ,则
,则![]() ;
;
②若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③“平面向量![]() 的夹角是钝角”的一个充分不必要条件是“
的夹角是钝角”的一个充分不必要条件是“![]() ”;
”;
④命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”.
”.
其中正确的个数是( )
A. 1B. 2C. 3D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,现有如下两种图象变换方案:
,现有如下两种图象变换方案:
(方案1):将函数![]() 的图象上所有点的横坐标变为原来的一半,纵坐标不变,再将所得图象向左平移
的图象上所有点的横坐标变为原来的一半,纵坐标不变,再将所得图象向左平移![]() 个单位长度;
个单位长度;
(方案2):将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再将所得图象上所有点的横坐标变为原来的一半,纵坐标不变.
个单位长度,再将所得图象上所有点的横坐标变为原来的一半,纵坐标不变.
请你从中选择一种方案,确定在此方案下所得函数![]() 的解析式,并解决如下问题:
的解析式,并解决如下问题:
(1)用“五点作图法”画出函数![]() 在
在![]() 的闭区间上的图象(列表并画图);
的闭区间上的图象(列表并画图);
(2)请你在答题纸相应位置逐一写出函数![]() 的①周期性②奇偶性③单调递增区间④单调递减区间.
的①周期性②奇偶性③单调递增区间④单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com