
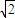 dn-1,n∈N*.
dn-1,n∈N*.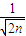 =0的距离为tn,证明:对?n∈N*,都有不等式:t1+t2+…+tn<
=0的距离为tn,证明:对?n∈N*,都有不等式:t1+t2+…+tn< 成立.
成立.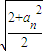 ,再根据an=
,再根据an=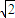 dn-1,可得dn=
dn-1,可得dn=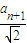 ,从而可得数列{
,从而可得数列{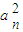 }是首项为2,公差为2的等差数列,进而可求数列{an}的通项公式;
}是首项为2,公差为2的等差数列,进而可求数列{an}的通项公式;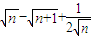 ,进而叠加,利用放缩法,即可证得结论.
,进而叠加,利用放缩法,即可证得结论.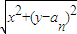 =
=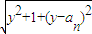 =
=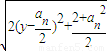 ,
,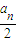 时,|PAn|取得最小值dn,且dn=
时,|PAn|取得最小值dn,且dn=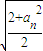 ,
,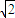 dn-1,∴an+1=
dn-1,∴an+1=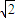 dn,∴dn=
dn,∴dn=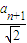
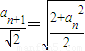
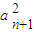 -
-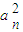 =2,又a=0,∴
=2,又a=0,∴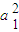 =2
=2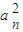 }是首项为2,公差为2的等差数列,所以
}是首项为2,公差为2的等差数列,所以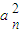 =2n,
=2n,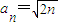 ;
;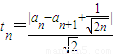 =
=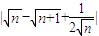 =
=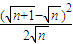

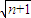 +
+ +
+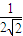 +…+
+…+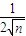
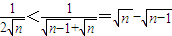
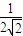 +…+
+…+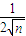 <
<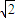 -1+
-1+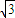 -
-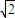 +…+
+…+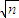 -
-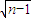 =
=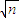 -1
-1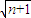 +
+ +
+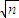 -1<
-1< .
.

科目:高中数学 来源: 题型:
| 2 |
| a1 |
| a3 |
| a3 |
| a5 |
| a2n-1 |
| a2n+1 |
| a2 |
| a4 |
| a4 |
| a6 |
| a2n |
| a2n+2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 1 | ||
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省揭阳一中高三(上)第二次段考数学试卷(解析版) 题型:解答题
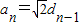 ,n∈N*.
,n∈N*.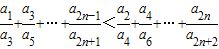 ;
;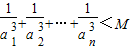 成立?请说明理由.
成立?请说明理由.查看答案和解析>>
科目:高中数学 来源:2012年广东省佛山市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,n∈N*.
,n∈N*. ;
; 成立?请说明理由.
成立?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com