【答案】
分析:(Ⅰ)根据曲线C:x
2-y
2=1上的点P到点A
n(0,a
n)的距离的最小值为d
n,设点P(x,y),利用两点间的距离公式,再采用配方法可得,再根据
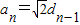
,可得
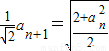
,从而可得
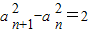
,从而数列
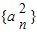
是首项
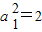
,公差为2的等差数列,进而可求数列{a
n}的通项公式;
(Ⅱ)先判断a
2n+2a
2n-1<a
2n+1a
2n,从而有
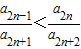
,所以
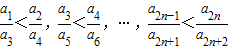
,叠加可得结论;
(Ⅲ)先证明
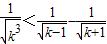
,从而可得
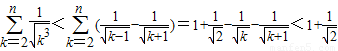
,进而可知存在常数
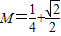
,对?n∈N
*,都有不等式:
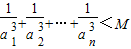
成立.
解答:(Ⅰ)解:设点P(x,y),则x
2-y
2=1,所以
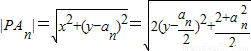
,
因为y∈R,所以当
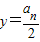
时,|PA
n|取得最小值d
n,且
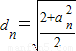
,
又
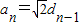
,所以
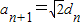
,即
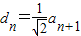
将
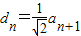
代入
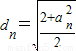
得
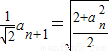
两边平方得
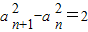
,又a
=0,
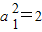
故数列
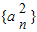
是首项
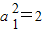
,公差为2的等差数列,所以
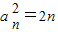
,
因为
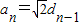
>0,所以
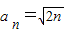
.…(6分)
(Ⅱ)证明:因为(2n+2)(2n-1)-2n(2n+1)=-2<0,
所以(2n+2)(2n-1)<2n(2n+1)
所以
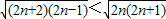
,所以a
2n+2a
2n-1<a
2n+1a
2n所以
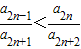
,所以
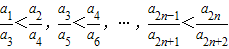
以上n个不等式相加得
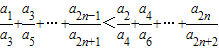
.…(10分)
(Ⅲ)解:因为
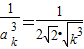
,当k≥2时,
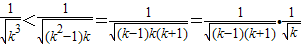
,
因为
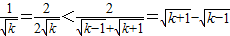
,
所以
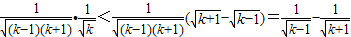
所以
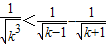
,
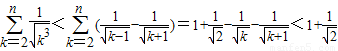
所以
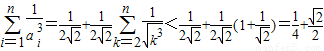
.
故存在常数
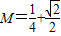
,对?n∈N
*,都有不等式:
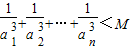
成立.…(14分)
点评:本题考查数列的通项,考查数列与不等式的综合,考查放缩法的运用,解题的关键是根据目标,适当放缩,难度较大.

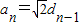 ,n∈N*.
,n∈N*.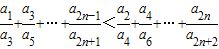 ;
;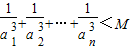 成立?请说明理由.
成立?请说明理由.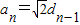 ,可得
,可得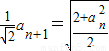 ,从而可得
,从而可得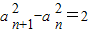 ,从而数列
,从而数列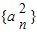 是首项
是首项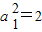 ,公差为2的等差数列,进而可求数列{an}的通项公式;
,公差为2的等差数列,进而可求数列{an}的通项公式;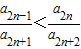 ,所以
,所以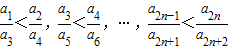 ,叠加可得结论;
,叠加可得结论;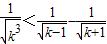 ,从而可得
,从而可得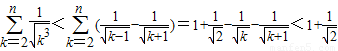 ,进而可知存在常数
,进而可知存在常数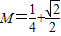 ,对?n∈N*,都有不等式:
,对?n∈N*,都有不等式: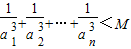 成立.
成立.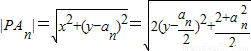 ,
,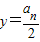 时,|PAn|取得最小值dn,且
时,|PAn|取得最小值dn,且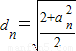 ,
,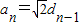 ,所以
,所以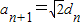 ,即
,即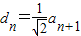
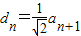 代入
代入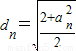 得
得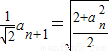
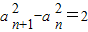 ,又a=0,
,又a=0,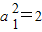
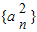 是首项
是首项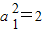 ,公差为2的等差数列,所以
,公差为2的等差数列,所以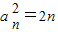 ,
,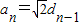 >0,所以
>0,所以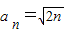 .…(6分)
.…(6分)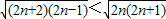 ,所以a2n+2a2n-1<a2n+1a2n
,所以a2n+2a2n-1<a2n+1a2n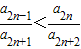 ,所以
,所以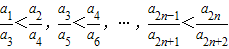
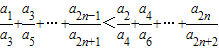 .…(10分)
.…(10分)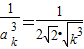 ,当k≥2时,
,当k≥2时,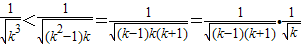 ,
,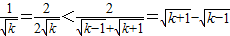 ,
,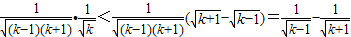
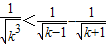 ,
,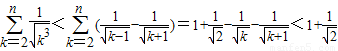
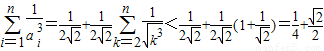 .
.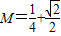 ,对?n∈N*,都有不等式:
,对?n∈N*,都有不等式: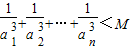 成立.…(14分)
成立.…(14分)

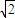 dn-1,n∈N*.
dn-1,n∈N*.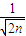 =0的距离为tn,证明:对?n∈N*,都有不等式:t1+t2+…+tn<
=0的距离为tn,证明:对?n∈N*,都有不等式:t1+t2+…+tn< 成立.
成立. ,n∈N*.
,n∈N*. ;
; 成立?请说明理由.
成立?请说明理由.