
【题目】已知a<0,解关于x的不等式ax2+(1﹣a)x﹣1>0.
【答案】解:原不等式可化为(ax+1)(x﹣1)>0,∵a<0,
∴(x+ ![]() )(x﹣1)<0,且不等式对应方程的两个实数根为﹣
)(x﹣1)<0,且不等式对应方程的两个实数根为﹣ ![]() 和1;
和1;
当﹣1<a<0时,﹣ ![]() >1,不等式的解集为{x|1<x<﹣
>1,不等式的解集为{x|1<x<﹣ ![]() };
};
当a=﹣1时,﹣ ![]() =1,不等式为(x﹣1)2<0,其解集为;
=1,不等式为(x﹣1)2<0,其解集为;
当a<﹣1时,﹣ ![]() <1,不等式的解集为{x|﹣
<1,不等式的解集为{x|﹣ ![]() <x<1}.
<x<1}.
【解析】对a分类讨论,先判断其相应方程的解集的情况,再把二次项的系数变为大于0,进而可求出不等式的解集.
【考点精析】认真审题,首先需要了解解一元二次不等式(求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】求适合下列条件的椭圆的标准方程:
(1)以(0,5)和(0,-5)为焦点,且椭圆上一点P到两焦点的距离之和为26;
(2)以椭圆9x2+5y2=45的焦点为焦点,且经过M(2, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,若sinA+sinB=sinC(cosA+cosB).
(1)判断△ABC的形状;
(2)在上述△ABC中,若角C的对边c=1,求该三角形内切圆半径的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
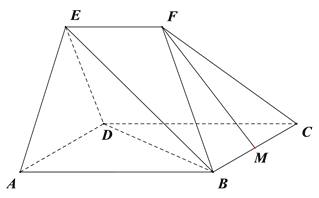
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记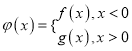 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
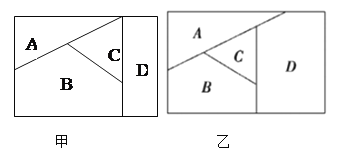
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x=3﹣ ![]() (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com