练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，圆的参数方程为（为参数），在以原点为极点，轴的非负半轴为极轴建立的极坐标系中，直线的极坐标方程为.

    （1）求圆的普通方程和直线的直角坐标方程；

    （2）设直线与轴，轴分别交于，两点，点是圆上任一点，求面积的最大值.

    【答案】（1），；（2）.

    【解析】

    （1）直接消元得到圆的普通方程，首先将直线的极坐标方程化简，再利用公式将极坐标方程转化为直角坐标方程；

    （2）首先求出直线与轴，轴的交点，设点的坐标为，表示出点到直线的距离，求出距离最值，再根据面积公式计算可得；

    解：（1）由消去参数，得，

    所以圆的普通方程为.

    由，得，

    所以直线的直角坐标方程为.

    （2）直线与轴，轴的交点为，，

    设点的坐标为，则点到直线的距离为

    ，

    所以，又，

    所以面积的最大值是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为计算， 设计了如图所示的程序框图，则空白框中应填入（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知若椭圆：（）交轴于，两点，点是椭圆上异于，的任意一点，直线，分别交轴于点，，则为定值.

    （1）若将双曲线与椭圆类比，试写出类比得到的命题；

    （2）判定（1）类比得到命题的真假，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆：的左、右焦点分别是，，离心率为，左、右顶点分别为，.过且垂直于轴的直线被椭圆截得的线段长为1.

    （1）求椭圆的标准方程；

    （2）经过点的直线与椭圆相交于不同的两点、（不与点、重合），直线与直线相交于点，求证：、、三点共线.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S- ABCD中，SD⊥底面ABCD，AB//DC，AD ⊥ DC,，AB=AD＝1DC=SD=2， E为棱SB上的一点，且SE=2EB．

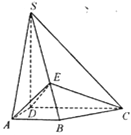
    (I)证明：DE⊥平面SBC；

    (II)证明：求二面角A- DE -C的大小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，且离心.

    （1）求椭圆的方程；

    （2）设，是椭圆上异于点的任意两点，直线，，的斜率分别为，，，且，试问当时，直线是否恒过一定点？若是，求出该定点的坐标；若不是，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的两个零点之差的绝对值的最小值为，将函数的图象向左平移个单位长度得到函数的图象，则下列说法正确的是（ ）

    ①函数的最小正周期为；②函数的图象关于点()对称；

    ③函数的图象关于直线对称；④函数在上单调递增.

    A.①②③④B.①②C.②③④D.①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：

    (1)取到的2只都是次品；

    (2)取到的2只中正品、次品各一只；

    (3)取到的2只中至少有一只正品、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双曲线 的左、右焦点分别为，过作倾斜角为的直线与轴和双曲线的右支分别交于两点，若点平分线段，则该双曲线的离心率是（ ）

    A. B. C. 2 D.

    查看答案和解析>>

    同步练习册答案