[题目]过曲线C1:-＝1的左焦点F1作曲线C2:x2+y2＝a2的切线.设切点为M.直线F1M交曲线C3:y2＝2px于点N.其中曲线C1与C3有一个共同的焦点.若|MF1|＝|MN|.则曲线C1的离心率为( )A. B. -1 C. +1 D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】过曲线C1：－＝1(a＞0，b＞0)的左焦点F1作曲线C2：x2＋y2＝a2的切线，设切点为M，直线F1M交曲线C3：y2＝2px(p＞0)于点N，其中曲线C1与C3有一个共同的焦点，若|MF1|＝|MN|，则曲线C1的离心率为( )

A. B. －1 C. ＋1 D.

【答案】D

【解析】设双曲线的右焦点为F2，则F2的坐标为(c，0)．

由题意知F2也是C3的焦点，所以C3：y2＝4cx.连接OM，NF2，因为O为F1F2的中点，M为F1N的中点，所以OM为△NF1F2的中位线，所以OM∥NF2.因为|OM|＝a，所以|NF2|＝2a.又NF2⊥NF1，|F1F2|＝2c，所以|NF1|＝2b.设N(x，y)，则由抛物线的定义可得|NF2|＝x＋c＝2a，所以x＝2a－c.过点F1作x轴的垂线，点N到该垂线的距离为2a，由y2＋4a2＝4b2，即4c(2a－c)＋4a2＝4(c2－a2)，得e2－e－1＝0，解得e＝ (负值舍去)，故选D.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】（I）若，恒成立，求常数的取值范.

（Ⅱ）已知非零常数、满足，求不等式的解集；

查看答案和解析>>

科目：高中数学 来源： 题型：

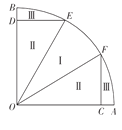
【题目】现有一个以、为半径的扇形池塘，在、上分别取点、，作、分别交弧于点、，且，现用渔网沿着、、、将池塘分成如图所示的养殖区域.已知，，（）.

（1）若区域Ⅱ的总面积为，求的值；

（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元，试问：当为多少时，年总收入最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设二次函数满足下列条件：

①对恒成立； ②对恒成立.

（1）求的值；（2）求的解析式；

（3）求最大的实数，使得存在实数，当时，恒成立.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知过点A(0，1)且斜率为k的直线l与圆C：(x－2)2＋(y－3)2＝1交于M，N两点．

(1)求k的取值范围；

(2)若＝12，其中O为坐标原点，求|MN|.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的中心在坐标原点，长轴在轴上，分别在其左、右焦点，在椭圆上任意一点，且的最大值为1，最小值为．

（1）求椭圆的方程；

（2）设为椭圆的右顶点，直线是与椭圆交于两点的任意一条直线，若，证明直线过定点．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据已往经验，潜水员下潜的平均速度为（米/单位时间），每单位时间的用氧量为（升），在水底作业10个单位时间，每单位时间用氧量为（升），返回水面的平均速度为（米/单位时间），每单位时间用氧量为（升），记该潜水员在此次考察活动中的总用氧量为（升）.