
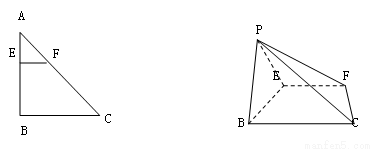
.(12分)如图,在Rt△ABC中,∠C=90º,BE平分∠ABC交AC于点E,点D在AB上,
DE⊥EB
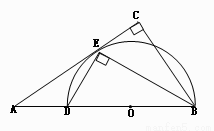
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=6,AE=6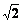 ,求BC的长。
,求BC的长。
(1) 见解析;(2) BC=4。
【解析】本题主要考查了切线的判定定理的应用,直角三角形基本关系的应用,属于基本知识的简单综合.
(Ⅰ)要证明AC是△BDE的外接圆的切线,故考虑取BD的中点O,只要证明OE⊥AC,结合∠C=90°,证明BC∥OE即可
(Ⅱ)设⊙O的半径为r,则在△AOE中,由OA2=OE2+AE2,可求r,代入可得OA,2OE,Rt△AOE中,可求∠A,∠AOE,进而可求∠CBE=∠OBE,在BCE中,通过EC与BE的关系可求
解:(1)取BD的中点O,连结OE
∵DE⊥EB
∴DB是△BED的外接圆的直径,
∴OE是⊙O的半径
∴BE平分∠ABC
∴∠ABE=∠EBC
∵OE=OB ∴∠ABE=∠DEO
∴∠DEO=∠EBC,∴EO∥BC
∵∠C=90º,∴∠AEO=90º ∴AC是⊙O的切线……….6分
(2)由(1)得:AE2=AD•AB
∴(6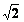 )2=6•AB,AB=12,∴OE=OD=3,AO=9
)2=6•AB,AB=12,∴OE=OD=3,AO=9
∵EO∥BC,∴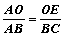 ,即
,即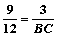 ,∴BC=4………12分
,∴BC=4………12分


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
(08年福建师大附中模拟)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 是正三角形,且平面
是正三角形,且平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 的中点
的中点
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求![]() 点到平面
点到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:2013届辽宁省分校高三12月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在四棱锥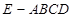 中,底面
中,底面 是矩形,
是矩形,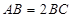 ,
,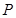 、
、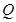 分别为线段
分别为线段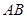 、
、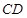 的中点,
的中点,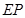 ⊥底面
⊥底面 .
.
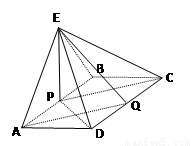
(Ⅰ)求证: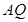 ∥平面
∥平面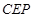 ;
;
(Ⅱ)求证:平面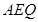 ^平面
^平面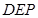 ;
;
(Ⅲ)若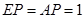 ,求三棱锥
,求三棱锥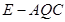 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省南阳市高三第八次周考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在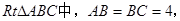 点
点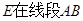 上,过点
上,过点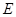 做
做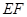 //
//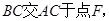 将
将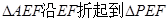 的位置(
的位置(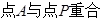 ),
),
使得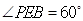 .
.
(I)求证: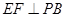 (II)试问:当点
(II)试问:当点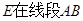 上移动时,二面角
上移动时,二面角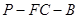 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省年高一下学期期末理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在几何体P-ABCD中,四边形ABCD为矩形,PA⊥平面ABCD,AB=PA=2.
(1)当AD=2时,求证:平面PBD⊥平面PAC;
(2)若PC与AD所成角为45°,求几何体P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省丹东市四校协作体高三第二次联合考试理科数学卷 题型:解答题
(本小题满分12分)
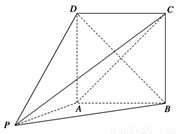
如图,在三棱锥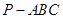 中,
中,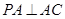 ,
,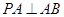 ,
,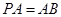 ,
,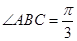 ,
,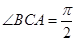 , 点
, 点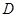 ,
,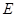 分别在棱
分别在棱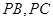 上,且
上,且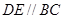 ,
,
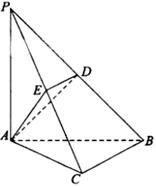
(I)求证: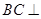 平面
平面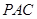 ;
;
(II)当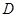 为
为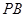 的中点时,求
的中点时,求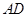 与平面
与平面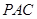 所成的角的大小;
所成的角的大小;
(III)是否存在点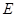 使得二面角
使得二面角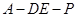 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com