练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，三棱锥中，平面平面，，且.

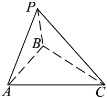
    （1）求证：；

    （2）若，求二面角的余弦值.

    【答案】（1）证明见解析（2）

    【解析】

    （1）取的中点，连接.根据，得 ，再由，根据线面垂直的判定定理得平面，则，再利用三线合一证明.

    （2）由三条直线两两垂直，建立空间直角坐标系，分别求得平面和平面的一个法向量，再利用二面角的向量法公式求解.

    （1）取的中点，连接.

    ，，

    平面，

    平面，

    又OC平面，，

    而是的中点，.

    （2）平面平面，平面，

    平面平面，

    平面，

    再由（1）可知三条直线两两垂直.

    以所在直线分别为x轴、y轴、z轴建立空间直角坐标系.

    由条件可得，.

    则，

    ，，.

    设平面的一个法向量为，

    由可得

    ，

    令，则.

    同理可得平面的一个法向量为，

    则.

    由图易知，二面角为锐角，

    二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为F1，F2，过点F1的直线与C交于A，B两点.△ABF2的周长为，且椭圆的离心率为.

    （1）求椭圆C的标准方程：

    （2）设点P为椭圆C的下顶点，直线PA，PB与y＝2分别交于点M，N，当|MN|最小时，求直线AB的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】棉花的优质率是以其纤维长度来街量的，纤维越长的棉花晶质越高.棉花的品质分类标准为:纤维长度小于等于的为粗绒棉，纤维长度在的为细绒棉，纤维长度大于的为长绒棉，其中纤维长度在以上的棉花又名“军海1号”.某采购商从新疆某一棉花基地抽测了根棉花的纤维长度，得到数据如下图频率分布表所示：

    纤维长度

    根数

    （1）若将频率作为概率， 根据以上数据，能否认为该基地的这批棉花符合“长绒棉占全部棉花的以上”的要求？

    （2）用样本估计总体， 若这批榨花共有,基地提出了两种销售方案给采购商参考.方案一：不分等级卖出，每千克按元计算，方案二:对棉花先分等级再销售，分级后不同等级的棉花售价如下表：

    纤维长度

    售价

    从来购商的角度，请你帮他决策一下该用哪个方案.

    （3）用分层抽样的方法从长绒棉中抽取6根棉花,再从此根棉花中抽取两根进行检验.求抽到的两根棉花只有一根是“军海1号”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知抛物线的焦点为，为上异于原点的任意一点，过点的直线交于另一点，交轴的正半轴于点，且有.当点的横坐标为时，为正三角形.

    （Ⅰ）求的方程；

    （Ⅱ）若直线，且和有且只有一个公共点，

    （ⅰ）证明直线过定点，并求出定点坐标；

    （ⅱ）的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，为矩形的边上一点，且，将沿折起到，使得.



    （1）证明：平面平面；

    （2）若，求平面与平面所成的锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，点是直线上的动点，为定点，点为的中点，动点满足，且，设点的轨迹为曲线.

    （1）求曲线的方程；

    （2）过点的直线交曲线于，两点，为曲线上异于，的任意一点，直线，分别交直线于，两点.问是否为定值？若是，求的值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系中，曲线的参数方程为（是参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）设曲线经过伸缩变换得到曲线，是曲线上任意一点，求点到曲线的距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本万元，且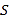．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．

    （1）求出2018年的利润L（x）（万元）关于年产量x（百辆）的函数关系式；（利润=销售额-成本）

    （2）2018年产量为多少百辆时，企业所获利润最大?并求出最大利润．

    查看答案和解析>>

    同步练习册答案