
【题目】已知圆![]() 与曲线
与曲线![]() 有三个不同的交点.
有三个不同的交点.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 是
是![]() 轴上的动点,
轴上的动点, ![]() ,
, ![]() 分别切圆
分别切圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若![]() ,求
,求![]() 及直线
及直线![]() 的方程;
的方程;
②求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ;②过定点
;②过定点![]() .
.
【解析】试题分析:(1)由![]() 得
得![]() 或
或![]() 。直线
。直线![]() 与圆
与圆![]() 相交,故直线
相交,故直线![]() 与圆
与圆![]() 相切,所以可用圆心到直线的距离等于
相切,所以可用圆心到直线的距离等于![]() ,可求得;(2)①设直线
,可求得;(2)①设直线![]() ,
, ![]() 交于点
交于点![]() ,由弦长、勾股定理可求|MP|,在直角三角形AMQ,由三角形相似得
,由弦长、勾股定理可求|MP|,在直角三角形AMQ,由三角形相似得![]() ,求得
,求得![]() ,设点
,设点![]() ,由距离公式求点
,由距离公式求点![]() 的坐标,再结合点M的坐标求直线MQ的方程;②设点
的坐标,再结合点M的坐标求直线MQ的方程;②设点![]() ,求过点Q、M的圆的方程,弦AB为两圆的公共弦,求直线AB的方程,由方程求定点的坐标。
,求过点Q、M的圆的方程,弦AB为两圆的公共弦,求直线AB的方程,由方程求定点的坐标。
试题解析:(1)因为直线![]() 与圆
与圆![]() 相切,
相切,
故圆心![]() 到直线的距离为
到直线的距离为![]() ,即:
,即: ![]() ,
, ![]() .
.
所以圆的方程为![]() .
.
(2)①设直线![]() ,
, ![]() 交于点
交于点![]() ,则
,则![]() ,
,
又![]() ,所以
,所以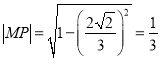 ,
,
而![]() ,所以
,所以![]() ,
,
设![]() ,而点
,而点![]() ,由
,由![]() ,
, ![]() ,
,
则![]() 或
或![]() ,
,
从而直线![]() 的方程为:
的方程为:
![]() 或
或![]() .
.
②证明:设点![]() ,由几何性质可以知道,
,由几何性质可以知道, ![]() ,
, ![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,
此圆的方程为![]() ,
, ![]() 为两圆的公共弦,
为两圆的公共弦,
两圆方程相减得![]() ,
,
即![]() ,
,
所以过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.

(1)求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)求当天的利润不低于750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船都要停靠在同一个泊位,它们可能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为4小时与2小时,求有一艘船停靠泊位时必需等待一段时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() .
.
(1)过点![]() 的直线
的直线![]() 与圆交与
与圆交与![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点记为
向该圆引一条切线,切点记为![]() ,
,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,求使得
,求使得![]() 取得最小值时点
取得最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各种情况下,向量终点构成什么图形?
(1)把所有单位向量的起点平移到同一点![]() ;
;
(2)把平行于某一直线的所有单位向量的起点平移到同一点;
(3)把平行于某一直线的一切向量平移到同一起点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为(25-x)万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=累计收入+销售收入-总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
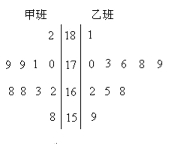
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某隧道设计为双向四车道,车道总宽为![]() ,要求通行车辆限高
,要求通行车辆限高![]() ,隧道全长为
,隧道全长为![]() ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.
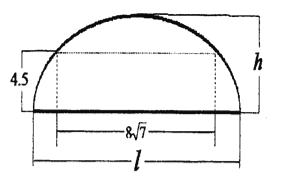
(1)若最大拱高![]() 为
为![]() ,则隧道设计的拱宽
,则隧道设计的拱宽![]() 是多少?
是多少?
(2)若最大拱高![]() 不小于
不小于![]() ,则应如何设计拱高
,则应如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?
(注: 1.半个椭圆的面积公式为![]() ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积![]() 隧道长)
隧道长)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com