练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

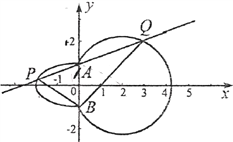
    【题目】如图，曲线由左半椭圆和圆在轴右侧的部分连接而成， ， 是与的公共点，点， （均异于点， ）分别是， 上的动点．

    （Ⅰ）若的最大值为，求半椭圆的方程；

    （Ⅱ）若直线过点，且， ，求半椭圆的离心率．

    【答案】(Ⅰ) ；(Ⅱ) .

    【解析】试题分析：(1)由题意可知，当为半椭圆与轴的左交点， 为圆与轴的右交点时， 会取得最大值，（2）设直线方程与圆组方程组，由韦达用k表示出Q点坐标，由，用k表示P点坐标，再由代入向量坐标运算，可求得斜率k及P点坐标，可得椭圆方程及离心率。

    试题解析;（Ⅰ）由已知得：当为半椭圆与轴的左交点， 为圆与轴的右交点时， 会取得最大值，即，解得，由图像可得，即，故半椭圆的方程为．

    （Ⅱ）设直线方程为， ， ，联立

    得，故， ， ，又，

    且， ，故， ， ，

    又，且， ，

    ，

    解得，故，代入解得，故．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】经过长期观察得到：在交通繁忙的时段内，某公路汽车的车流量（千辆/小时）与汽车的平均速度（千米/小时）之间的函数关系为

    （1）在该时段内，当汽车的平均速度为多少时，车流量最大，最大车流量为多少？（精确到0．1千辆/小时）

    （2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （Ⅰ）当时，求函数的单调递减区间；

    （Ⅱ）若时，关于的不等式恒成立，求实数的取值范围；

    （Ⅲ）若数列满足， ，记的前项和为，求证： .

    【答案】（I）；（II）；（III）证明见解析.

    【解析】试题分析：（Ⅰ）求出，在定义域内，分别令求得的范围，可得函数增区间， 求得的范围，可得函数的减区间；（Ⅱ）当时，因为，所以显然不成立，先证明因此时， 在上恒成立，再证明当时不满足题意，从而可得结果；（III）先求出等差数列的前项和为，结合（II）可得，各式相加即可得结论.

    试题解析：（Ⅰ）由，得.所以

    令，解得或（舍去），所以函数的单调递减区间为 .

    （Ⅱ）由得，

    当时，因为，所以显然不成立，因此.

    令，则，令，得.

    当时， ， ，∴，所以，即有.

    因此时， 在上恒成立.

    ②当时， ， 在上为减函数，在上为增函数，

    ∴，不满足题意.

    综上，不等式在上恒成立时，实数的取值范围是.

    （III）证明：由知数列是的等差数列，所以

    所以

    由（Ⅱ）得， 在上恒成立.

    所以. 将以上各式左右两边分别相加，得

    .因为

    所以

    所以.

    【题型】解答题
    【结束】
    22

    【题目】已知直线， (为参数， 为倾斜角).以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的直角坐标方程为.

    （Ⅰ）将曲线的直角坐标方程化为极坐标方程；

    （Ⅱ）设点的直角坐标为，直线与曲线的交点为、，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨，黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查，随机抽取80名群众进行调查，将他们的年龄分成6段： ,,,， ， ，得到如图所示的频率分布直方图.问：

    （Ⅰ）求这80名群众年龄的中位数；

    （Ⅱ）若用分层抽样的方法从年龄在中的群众随机抽取6名，并从这6名群众中选派3人外出宣传黔东南，求选派的3名群众年龄在的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ln (x＋1)－ －x，a∈R.

    (1)当a>0时，求函数f(x)的单调区间；

    (2)若存在x>0，使f(x)＋x＋1<－ (a∈Z)成立，求a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点，点是单位圆与轴的正半轴的交点.

    （1）若，求.

    （2）已知，，若是等边三角形，求的面积.

    （3）设点为单位圆上的动点，点满足，，，求的取值范围.当时，求四边形的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4－4：坐标系与参数方程]

    在直角坐标系中，曲线的参数方程为（为参数），直线的参数方程为（为参数）.

    （1）求和的直角坐标方程；

    （2）若曲线截直线所得线段的中点坐标为，求的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在边长为8的正三角形ABC中，E，F依次是AB，AC的中点，，D，H，G为垂足，若将绕AD旋转，求阴影部分形成的几何体的表面积与体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线经过点．

    (1)若原点到直线的距离为2，求直线的方程；

    (2)若直线被两条相交直线和所截得的线段恰被点平分，求直线的方程．

    查看答案和解析>>

    同步练习册答案