练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】经过长期观察得到：在交通繁忙的时段内，某公路汽车的车流量（千辆/小时）与汽车的平均速度（千米/小时）之间的函数关系为

    （1）在该时段内，当汽车的平均速度为多少时，车流量最大，最大车流量为多少？（精确到0．1千辆/小时）

    （2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？

    【答案】（1）速度30时，最大车流量为11．3；（2）

    【解析】

    试题（1）将车流量y与汽车的平均速度v之间的函数关系（v＞0）化简为，应用基本不等式即可求得v为多少时，车流量最大及最大车流量；（2）依题意，解不等式，即可求得答案

    试题解析：（1）由题意有

    当且仅当，即时上式等号成立，

    此时（千辆/小时）

    （2）由条件得，整理得，

    即 ，∴

    故当千米/小时时车流量最大，且最大车流量为11．3千辆/小时

    若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在所表示的范围内．（12分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】扎比瓦卡是2018年俄罗斯世界杯足球赛吉祥物，该吉祥物以西伯利亚平原狼为蓝本.扎比瓦卡，俄语意为“进球者”.某厂生产“扎比瓦卡”的固定成本为15000元，每生产一件“扎比瓦卡”需要增加投入20元，根据初步测算，每个销售价格满足函数，其中x是“扎比瓦卡”的月产量（每月全部售完）.

    （1）将利润表示为月产量的函数；

    （2）当月产量为何值时，该厂所获利润最大？最大利润是多少？（总收益=总成本+利润）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中,底面是边长为的菱形,侧面底面,, , 是中点,点在侧棱上.

    （Ⅰ）求证: ;

    （Ⅱ）若是中点,求二面角的余弦值;

    （Ⅲ）是否存在,使平面?若存在,求出的值;若不存在,说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.点（2，0）关于直线y＝x+1的对称点为（﹣1，3）

    B.过（x1，y1），（x2，y2）两点的直线方程为

    C.经过点（1，1）且在x轴和y轴上截距都相等的直线方程为x+y﹣2＝0或x﹣y＝0

    D.直线x﹣y﹣4＝0与两坐标轴围成的三角形的面积是8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明家的晚报在下午任何一个时间随机地被送到，他们一家人在下午任何一个时间随机地开始晚餐．为了计算晚报在晚餐开始之前被送到的概率，某小组借助随机数表的模拟方法来计算概率，他们的具体做法是将每个1分钟的时间段看作个体进行编号，编号为01，编号为02，依此类推，编号为90．在随机数表中每次选取一个四位数，前两位表示晚报时间，后两位表示晚餐时间，如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义，视为这次读取的无效数据（例如下表中的第一个四位数6548中的65不符合晚报时间）．按照从左向右，读完第一行，再从左向右读第二行的顺序，读完下表，用频率估计晚报在晚餐开始之前被送到的概率为（ ）

    6548 1176 7417 4685 0950 5804 7769 7473 0395 7186

    8012 4356 3517 7270 8015 4531 8223 7421 1157 8263

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴上，离心率等于，它的一个顶点恰好在抛物线的准线上．

    求椭圆的标准方程；

    点，在椭圆上，是椭圆上位于直线两侧的动点当运动时，满足，试问直线的斜率是否为定值，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥S﹣ABCD中，底面ABCD是边长为4的菱形，∠BAD＝60°，SA＝SD＝2，点E是棱AD的中点，点F在棱SC上，且λ，SA//平面BEF．

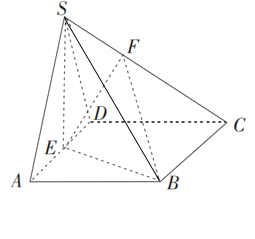
    （1）求实数λ的值；

    （2）求三棱锥F﹣EBC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“我将来要当一名麦田里的守望者，有那么一群孩子在一块麦田里玩，几千万的小孩子，附近没有一个大人，我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形的麦田里成为守望者，如图所示，为了分割麦田，他将连接，设中边所对的角为，中边所对的角为，经测量已知，.

    （1）霍尔顿发现无论多长，为一个定值，请你验证霍尔顿的结论，并求出这个定值；

    （2）霍尔顿发现麦田的生长于土地面积的平方呈正相关，记与的面积分别为和，为了更好地规划麦田，请你帮助霍尔顿求出的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

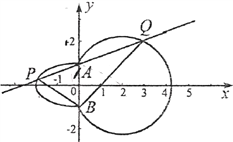
    【题目】如图，曲线由左半椭圆和圆在轴右侧的部分连接而成， ， 是与的公共点，点， （均异于点， ）分别是， 上的动点．

    （Ⅰ）若的最大值为，求半椭圆的方程；

    （Ⅱ）若直线过点，且， ，求半椭圆的离心率．

    查看答案和解析>>

    同步练习册答案