
【题目】如图所示,正方形![]() 边长为
边长为![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小为
的大小为![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在直线
在直线![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角正弦值为
所成角正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据已知可得![]() ,证明得
,证明得![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)由(1)得![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() ,建立如下图直角坐标系,得出
,建立如下图直角坐标系,得出![]() 坐标,设
坐标,设![]() ,由已知条件结合直线与平面所成角公式,求出
,由已知条件结合直线与平面所成角公式,求出![]() ,确定
,确定![]() 坐标,分别求出平面
坐标,分别求出平面![]() 和平面
和平面![]() 法向量坐标,再由空间向量的二面角公式,即可求解.
法向量坐标,再由空间向量的二面角公式,即可求解.
(1)证明:设![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,即
,即![]() 为
为![]() 中点,
中点,
又因为![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]()
由于![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为![]() ,
,
所以![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() ,
,
得![]() ,由
,由![]() ,
,![]()
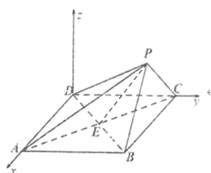
以![]() 点为原点建立如图空间直角坐标系
点为原点建立如图空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,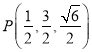 ,
,
设![]() ,
,
所以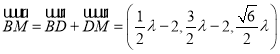
平面![]() 的一个法向量可为
的一个法向量可为![]() ,
,
因为直线![]() 与平面
与平面![]() 所成角正弦值为
所成角正弦值为![]()
所以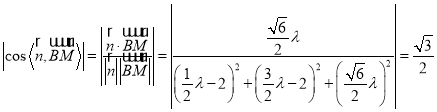 ,
,
解得![]() ,所以
,所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则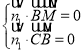 ,
,
即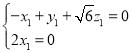 ,令
,令![]() ,得
,得![]() ,
,
因为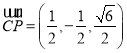 ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则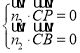 ,
,
即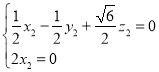 ,令
,令![]() ,得
,得![]() ,
,
所以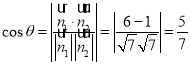 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,边长为1的正方形区域OABC内有以OA为半径的圆弧![]() .现决定从AB边上一点D引一条线段DE与圆弧
.现决定从AB边上一点D引一条线段DE与圆弧![]() 相切于点E,从而将正方形区域OABC分成三块:扇形COE为区域I,四边形OADE为区域II,剩下的CBDE为区域III.区域I内栽树,区域II内种花,区域III内植草.每单位平方的树、花、草所需费用分别为
相切于点E,从而将正方形区域OABC分成三块:扇形COE为区域I,四边形OADE为区域II,剩下的CBDE为区域III.区域I内栽树,区域II内种花,区域III内植草.每单位平方的树、花、草所需费用分别为![]() 、
、![]() 、
、![]() ,总造价是W,设
,总造价是W,设![]()

(1)分别用![]() 表示区域I、II、III的面积;
表示区域I、II、III的面积;
(2)将总造价W表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(3)求![]() 为何值时,总造价W取最小值?
为何值时,总造价W取最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.

(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国.中国自古便有十天干与十二地支.十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸,十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如说第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”… …依此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”“乙亥”,之后地支回到“子”重新开始,即“丙子”… …依此类推.1911年中国爆发推翻清朝专制帝制、建立共和政体的全国性革命,这一年是辛亥年,史称“辛亥革命”.1949新中国成立,请推算新中国成立的年份为( )
A.己丑年B.己酉年
C.丙寅年D.甲寅年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若以该直角坐标系的原点为极点,
为参数),若以该直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和
和![]() 有且仅有一个公共点,求
有且仅有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒),人传人,传播快,传播广,病亡率高,对人类生命形成巨大危害.在中华人民共和国,在中共中央、国务院强有力的组织领导下,全国人民万众一心抗击、防控新冠肺炎,疫情早在3月底已经得到了非常好的控制(累计病亡人数3869人).然而,国外因国家体制、思想观念与中国的不同,防控不力,新冠肺炎疫情越来越严重.据美国约翰斯·霍普金斯大学每日下午6时公布的统计数据,选取5月6日至5月10日的美国的新冠肺炎病亡人数如下表(其中t表示时间变量,日期“5月6日”、“5月7日”对应于“t=6"、“t=7",依次下去),由下表求得累计病亡人数与时间的相关系数r=0.98.
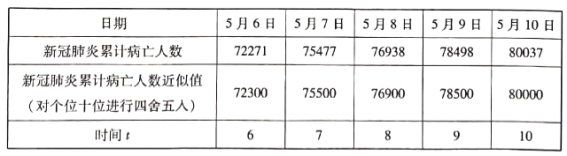
(1)在5月6日~10日,美国新冠肺炎病亡人数与时间(日期)是否呈现线性相关性?
(2)选择对累计病亡人数四舍五入后个位、十位均为0的近似数,求每日累计病亡人数y随时间t变化的线性回归方程;
(3)请估计美国5月11日新冠肺炎病亡累计人数,请初步预测病亡人数达到9万的日期.
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为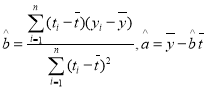
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com