练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
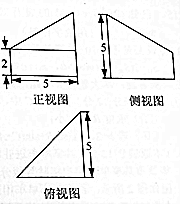
    17．《九章算术》是中国古代第一部数学专著，书中有关于“堑堵”的记载，“堑堵”即底面是直角三角形的直三棱柱，已知某“堑堵”被一个平面截去一部分后，剩下部分的三视图如图所示，则剩下部分的体积是（　　）
    A．50B．75C．25.5D．37.5

    分析 由题意，几何体是直三棱柱截去一个四棱锥，由此计算体积．

    解答 解：由已知得到几何体为直三棱柱截去一个四棱锥，如图：体积为$\frac{1}{2}×5×5×5-\frac{1}{3}×5×3×5=\frac{75}{2}$=37.5；
    故选：D．

    点评 本题考查了几何体的三视图；由三视图求对应几何体的体积，关键是正确还原几何体．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．已知$\overrightarrow a=（{1，λ}），\overrightarrow b=（{2，1}）$，若向量$2\overrightarrow a+\overrightarrow b$与$\overrightarrow c=（{8，6}）$共线，则$\overrightarrow a$在$\overrightarrow b$方向上的投影为$\frac{3\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1、F2，A为椭圆E的右顶点，B，C分别为椭圆E的上、下顶点．线段CF2的延长线与线段AB交于点M，与椭圆E交于点P．
    （1）若椭圆的离心率为$\frac{{\sqrt{2}}}{2}$，△PF1C的面积为12，求椭圆E的方程；
    （2）设S${\;}_{△CM{F}_{2}}$=λ•S${\;}_{△CP{F}_{1}}$，求实数λ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数p（x）=lnx-x+4，q（x）=$\frac{{a{e^x}}}{x}（{a∈R}）$．
    （1）若函数y=p（x），y=q（x）的图象有平行于坐标轴的公切线，求a的值；
    （2）若关于x的不等式p（x）-4＜q（x）的解集中有且只有两个整数，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=（2x-1）ex，a=f（1），b=f（-$\sqrt{2}$），c=f（-ln2），d=f（-$\frac{1}{2}$），则（　　）
    A．a＞b＞c＞dB．b＞a＞c＞dC．d＞a＞b＞cD．a＞d＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．定义在R上的函数f（x）的反函数为f-1（x），且对任意的x都有f（x）+f（6-x）=2，则f-1（1）=（　　）
    A．3B．2C．6D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

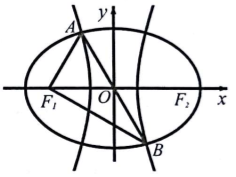    9．如图，F1、F2是椭圆C1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若AF1⊥BF1，且∠AF1O=$\frac{π}{3}$，则C1与C2的离心率之和为（　　）
    A．2$\sqrt{3}$B．4C．2$\sqrt{5}$D．2$\sqrt{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率$\frac{\sqrt{2}}{2}$，且P（0，1）是椭圆C上的点，F是椭圆的右焦点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）过点F且不与坐标轴平行的直线l与椭圆C交于A，B两点，线段AB的中点为M，O为坐标原点，直线OM的斜率kOM=-$\frac{1}{2}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．关于随机对照试验的说法，错误的是（　　）
    A．试验组的对象必须是随机选取的
    B．必须有试验组和对照组
    C．对照组中的对象不必使用安慰剂
    D．在有些随机对照试验中，为了得到更真实的结果，有时还需要使用安慰剂

    查看答案和解析>>

    同步练习册答案