
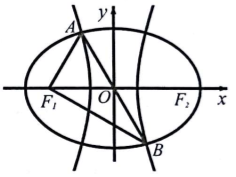
 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
分析 利用椭圆的对称性,求出椭圆的离心率,然后求解双曲线的离心率即可.
解答 解:F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,
若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,可得:A($-\frac{1}{2}c$,$\frac{\sqrt{3}}{2}c$),B($\frac{1}{2}c$,$-\frac{\sqrt{3}}{2}c$),
代入椭圆方程可得:$\frac{{c}^{2}}{4{a}^{2}}+\frac{3{c}^{2}}{4{b}^{2}}=1$,可得$\frac{{e}^{2}}{4}$+$\frac{3}{\frac{4}{{e}^{2}}-4}=1$,
可得e4-8e2+4=0,解得e=$\sqrt{3}-1$.
代入双曲线方程可得:$\frac{{c}^{2}}{4{a}^{2}}-\frac{3{c}^{2}}{4{b}^{2}}=1$,
可得:$\frac{{e}^{2}}{4}-\frac{3}{4-\frac{4}{{e}^{2}}}=1$,
可得:e4-8e2+4=0,解得e=$\sqrt{3}+1$,
则C1与C2的离心率之和为:2$\sqrt{3}$.
故选:A.
点评 本题考查椭圆以及双曲线的简单性质的应用,离心率的求法,注意椭圆以及双曲线的对称性的应用是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | $-\frac{7}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
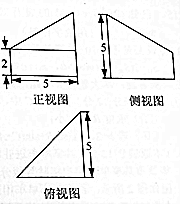 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )| A. | 50 | B. | 75 | C. | 25.5 | D. | 37.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
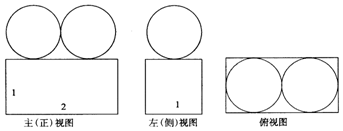
| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 数据 | 31,12,22,15,20,45,47,32,34,23,28 |
| A. | 23、32 | B. | 34、35 | C. | 28、32 | D. | 28、35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a不能被2017整除 | B. | b不能被2017整除 | ||
| C. | a、b都不能被2017整除 | D. | a、b中至多有一个能被2017整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 14种 | C. | 16种 | D. | 24种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com