
【题目】设点![]() 为抛物线
为抛物线![]() 上的动点,
上的动点,![]() 是抛物线的焦点,当
是抛物线的焦点,当![]() 时,
时,![]() .
.
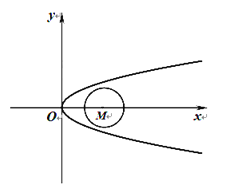
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() :
:![]() 的切线
的切线![]() ,
,![]() ,分别交抛物线
,分别交抛物线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)最小值
(2)最小值![]() .
.
【解析】
(1)利用抛物线的焦半径公式求得![]() 值,进而得到抛物线方程;
值,进而得到抛物线方程;
(2)设过点![]() 的切线为
的切线为![]() ,利用圆心到直线的距离等于半径得到
,利用圆心到直线的距离等于半径得到![]() ,化简并借助韦达定理,可得
,化简并借助韦达定理,可得![]() ,
,![]() ,设
,设![]() ,则直线
,则直线![]() ,与抛物线联立,再由根与系数的关系可得
,与抛物线联立,再由根与系数的关系可得![]() ,同理
,同理![]() ,再设直线
,再设直线![]() ,利用弦长公式求弦长,由点到直线距离公式求
,利用弦长公式求弦长,由点到直线距离公式求![]() 到直线
到直线![]() 的距离,代入三角形面积公式,换元后利用基本不等式和二次函数求最小值.
的距离,代入三角形面积公式,换元后利用基本不等式和二次函数求最小值.
(1)当![]() 时,
时,![]() ,
,
所以![]() ,故所求抛物线方程为
,故所求抛物线方程为![]() .
.
(2)点![]() 为抛物线
为抛物线![]() 上的动点,则
上的动点,则![]() ,
,
设过点![]() 的切线为
的切线为![]() ,
,
则![]() ,
,
得![]() ,
,
![]() 是方程(*)式的两个根,
是方程(*)式的两个根,
所以![]() ,
,![]() ,
,
设![]() ,
,
因直线![]() ,与抛物线
,与抛物线![]() 交于点A,
交于点A,
则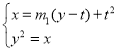 得
得![]() ,
,
所以![]() ,即
,即![]() ,
,
同理![]() ,
,
设直线![]() ,
,
则![]() ,
,
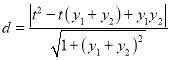 ,
,
又![]() ,
,
![]() ,
,
所以![]()
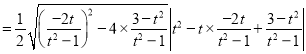

令![]() ,
,![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(1)试估计![]() 岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
(2)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: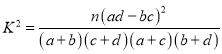 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆的左右焦点,点
分别为椭圆的左右焦点,点![]() 为椭圆
为椭圆![]() 上的一动点,
上的一动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,点
,点![]() ,证明:直线
,证明:直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
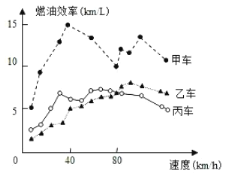
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com