
【题目】已知函数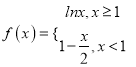 ,若
,若![]() 有两个零点
有两个零点![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】当x1时,f(x)=lnx0,
∴f(x)+11,
∴f[f(x)+1]=ln(f(x)+1),
当x<1,f(x)=1![]() >
>![]() ,f(x)+1>
,f(x)+1>![]() ,
,
f[f(x)+1]=ln(f(x)+1),
综上可知:F[f(x)+1]=ln(f(x)+1)+m=0,
则f(x)+1=em,f(x)=em1,有两个根![]() ,(不妨设
,(不妨设![]() <
<![]() ),
),
当x1是,ln![]() =em1,当x<1时,1
=em1,当x<1时,1![]() =em1,
=em1,
令t=em1>![]() ,则ln
,则ln![]() =t,
=t, ![]() =et,1
=et,1![]() =t,
=t, ![]() =22t,
=22t,
∴![]() =et(22t),t>
=et(22t),t>![]() ,
,
设g(t)=et(22t),t>![]() ,
,
求导g′(t)=2tet,
t∈(![]() ,+∞),g′(t)<0,函数g(t)单调递减,
,+∞),g′(t)<0,函数g(t)单调递减,
∴g(t)<g(![]() )
)![]() ,
,
∴g(x)的值域为(∞, ![]() ),
),
∴![]() 取值范围为(∞,
取值范围为(∞, ![]() ),
),
故选:D.


科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 和
和![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,射线
两点,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax-alnx(a∈R).
(1)若函数f(x)在x=1处取得极值,求a的值;
(2)在(1)的条件下,求证:f(x)≥-![]() +
+![]() -4x+
-4x+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD, ![]() ,M为PC的中点,N点在AB上且
,M为PC的中点,N点在AB上且![]() .
.
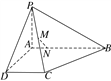
(1)证明:MN∥平面PAD;
(2)求直线MN与平面PCB所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
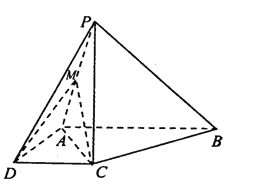
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com