
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 中点.
中点.
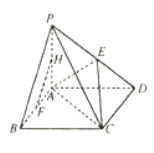
(1)证明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 底面
底面![]() ,
, ![]() ,试在
,试在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() ,并证明此结论.
,并证明此结论.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,证得
,证得![]() ,又
,又![]() 是
是![]() 的中点,证得
的中点,证得![]() ,利用线面平行的判定定理,即可证明,
,利用线面平行的判定定理,即可证明, ![]() 平面
平面![]() .
.
(2)连接![]() ,证得四边形
,证得四边形![]() 为平行四边形,得
为平行四边形,得![]() ,进而得到
,进而得到![]() 平面
平面![]() ,进而得
,进而得![]() ,
, ![]() ,利用线面垂直的判定定理,即可得
,利用线面垂直的判定定理,即可得![]() 平面
平面![]() .
.
试题解析:
(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵四边形![]() 为矩形,
为矩形,
∴![]() 为
为![]() 的中点.
的中点.
又![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 中点,∴
中点,∴![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解: ![]() 的中点
的中点![]() 即为所求的点.
即为所求的点.
证明如下:
连接![]() ,
,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
, ![]() .
.
又![]() 为
为![]() 的中点,且四边形
的中点,且四边形![]() 为矩形,
为矩形,
∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() .∴
.∴![]() .
.
又∵![]() ,
, ![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是
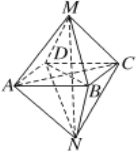
A. 该几何体是由两个同底的四棱锥组成的几何体
B. 该几何体有12条棱、6个顶点
C. 该几何体有8个面,并且各面均为三角形
D. 该几何体有9个面,其中一个面是四边形,其余均为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 、圆
、圆![]() 均满足圆心在直线
均满足圆心在直线![]() :
: ![]() 上,过点
上,过点![]() ,且与直线l2:x=-1相切.
,且与直线l2:x=-1相切.
(1)当![]() 时,求圆
时,求圆![]() ,圆
,圆![]() 的标准方程;
的标准方程;
(2)直线l2与圆![]() 、圆
、圆![]() 分别相切于A,B两点,求
分别相切于A,B两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω>0),将函数y=|f(x)|的图象向左平移
cosωx(ω>0),将函数y=|f(x)|的图象向左平移 ![]() 个单位长度后关于y轴对称,则当ω取最小值时,g(x)=cos(ωx+
个单位长度后关于y轴对称,则当ω取最小值时,g(x)=cos(ωx+ ![]() )的单调递减区间为( )
)的单调递减区间为( )
A.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
B.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
C.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
D.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
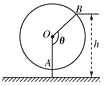
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,并且
的前n项和,并且![]() ,对任意正整数n,
,对任意正整数n, ![]() ;设
;设
![]() .
.
(Ⅰ) 证明:数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(Ⅱ) 设![]() ,求证: 数列
,求证: 数列![]() 不可能为等比数列。
不可能为等比数列。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com