【题目】设函数
．
（
）求不等式
的解集．
（
）若对于
， 
恒成立，求
的取值范围．
【答案】（1）当
时，解集为
；当
时，解集为
，当
时，解集为
；（2）
.
【解析】试题分析：（1）不等式
等价于
，分三种情况讨论，当
时，当
时，当
时，分别利用一元二次不等式的解法求解即可；（2）对任意的
， 
恒成立，等价于
，设
，则
在
上单调减， 
，从而可得
， 
．
试题解析：（
）解：∵
，∴
，当
时，解为： 
，当
时，解为： 
，当
时，解为： 
，综上：当
时，解集为
；当
时，解集为
，当
时，解集为
．
（
）∵对任意的
， 
恒成立， 
，设： 
，则
在
上单调减，
则： 
，∴
， 
．
【方法点晴】本题主要考查一元二次不等式的解法以及不等式恒成立问题、分类讨论思想的应用，属于中档题．不等式恒成立问题常见方法：① 分离参数
恒成立(
即可)或
恒成立（
即可）；② 数形结合(
图象在
上方即可)；③ 讨论最值
或
恒成立；④ 讨论参数.本题是利用方法 ① 求得
的取值范围.
小学课时特训系列答案科目：高中数学 来源： 题型：
【题目】对于数列
，设
表示数列
前
项
， 
， 
， 
中的最大项．数列
满足： 
．
（
）若
，求
的前
项和．
（
）设数列
为等差数列，证明： 
或者
（
为常数），
， 
， 
， 
．
（
）设数列
为等差数列，公差为
，且
．
记
，
求证：数列
是等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A={x|4x﹣1|＜9，x∈R}，B={x| 
≥0，x∈R}，则（RA）∩B=（ ）
A.（﹣∞，﹣3）∪[ 
，+∞）
B.（﹣3，﹣2]∪[0， ）??
C.（﹣∞，﹣3]∪[ ，+∞）
D.（﹣3，﹣2]
查看答案和解析>>
科目：高中数学 来源： 题型：
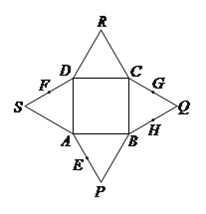
【题目】如图，已知四边形
是正方形， 
， 
， 
， 
都是等边三角形， 
、
、
、
分别是线段
、
、
、
的中点，分别以
、
、
、
为折痕将四个等边三角形折起，使得
、
、
、
四点重合于一点
，得到一个四棱锥．对于下面四个结论：
①
与
为异面直线； ②直线
与直线
所成的角为
③
平面
； ④平面
平面
；
其中正确结论的个数有（ ）
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知圆
的方程为： 
，直线
的方程为
．
（
）当
时，求直线
被圆
截得的弦长；
（
）当直线
被圆
截得的弦长最短时，求直线
的方程；
（
）在（
）的前提下，若
为直线
上的动点，且圆
上存在两个不同的点到点
的距离为
，求点
的横坐标的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
=1（a＞b＞0）过点（ 
，1），且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形．
（1）求椭圆的标准方程；
（2）设M（x，y）是椭圆C上的动点，P（p，0）是x轴上的定点，求|MP|的最小值及取最小值时点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
