【题目】以下有四个说法：
①若
、
为互斥事件，则
；
②在
中，
，则
；
③
和
的最大公约数是
；
④周长为
的扇形，其面积的最大值为
；
其中说法正确的个数是（ ）
A.
B.
C.
D.
【答案】C
【解析】
设
、
为对立事件可得出命题①的正误；利用大边对大角定理和余弦函数在
上的单调性可判断出命题②的正误；列出
和
各自的约数，可找出两个数的最大公约数，从而可判断出命题③的正误；设扇形的半径为
，再利用基本不等式可得出扇形面积的最大值，从而判断出命题④的正误.
对于命题①，若、为对立事件，则、互斥，则
，命题①错误；
对于命题②，由大边对大角定理知，
，且
，函数
在上单调递减，所以，
，命题②正确；
对于命题③，的约数有
、
、
、
、
、，的约数有、
、、
、
、
、
、，则和的最大公约数是，命题③正确；
对于命题④，设扇形的半径为，则扇形的弧长为
，
扇形的面积为
，由基本不等式得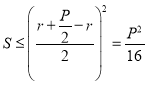
，
当且仅当
，即当
时，等号成立，所以，扇形面积的最大值为
，命题④错误.故选：C.
世纪百通优练测系列答案
百分学生作业本题练王系列答案科目：高中数学 来源： 题型：
【题目】有
件产品，其中
件是次品，其余都是合格品，现不放回的从中依次抽
件.求：（1）第一次抽到次品的概率；
（2）第一次和第二次都抽到次品的概率；
（3）在第一次抽到次品的条件下，第二次抽到次品的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面上， 
⊥ 
，| 
|=| 
|=1， 
= + ．若| 
|＜ 
，则| 
|的取值范围是（ ）
A.（0， 
]
B.（ ， 
]
C.（ ， 
]
D.（ ， ]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（sinx，﹣1）， 
=（2cosx，1）．
（1）若 ∥ ，求tanx的值；
（2）若 ⊥ ，又x∈[π，2π]，求sinx+cosx的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
