
若函数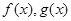 都在区间
都在区间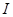 上有定义,对任意
上有定义,对任意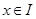 ,都有
,都有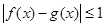 成立,则称函数
成立,则称函数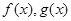 为区间
为区间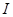 上的“伙伴函数”
上的“伙伴函数”
(1)若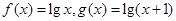 为区间
为区间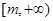 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断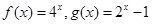 是否为区间
是否为区间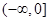 上的“伙伴函数”?
上的“伙伴函数”?
(3)若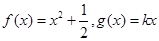 为区间
为区间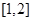 上的“伙伴函数”,求
上的“伙伴函数”,求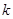 的取值范围
的取值范围
(1) ;(2)它们是“伙伴函数”;(3)
;(2)它们是“伙伴函数”;(3) 。
。
【解析】
试题分析:(1)由已知:
所以 ,解出:
,解出: ,从而
,从而
(2)由已知: ,其中
,其中
由二次函数的图像可知:当 时,
时,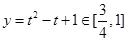
所以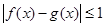 恒成立,所以它们是“伙伴函数”
恒成立,所以它们是“伙伴函数”
(3)由已知: 在
在 时恒成立。
时恒成立。
即: 在
在 时恒成立,分离参数可得:
时恒成立,分离参数可得:
 在
在 时恒成立,所以
时恒成立,所以
函数 在
在 时单调递增,所以其最大值为
时单调递增,所以其最大值为
函数 为双勾函数,利用图像可知其最小值为
为双勾函数,利用图像可知其最小值为 所以
所以 。
。
考点:本题主要考查指数函数、对数函数的性质,恒成立问题解法。
点评:难题,本题以新定义函数的形式,重点考查指数函数、对数函数及二次函数的性质,恒成立问题解法。对于“恒成立问题”往往转化成求函数的最值问题。本题利用了“分离参数法”。


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
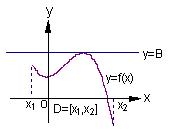
如右图(1)所示,定义在区间![]() 上的函数
上的函数![]() ,如果满
,如果满
足:对![]() ,
,![]() 常数A,都有
常数A,都有![]() 成立,则称函数
成立,则称函数
![]() 在区间
在区间![]() 上有下界,其中
上有下界,其中![]() 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数![]() 、
、![]() 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
 (Ⅰ)试判断函数
(Ⅰ)试判断函数![]() 在
在![]() 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间![]() 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数![]() 在区间
在区间![]() 上
上
有上界的定义,并判断(Ⅰ)中的函数在![]() 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数![]() 在区间
在区间![]() 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数
![]() 在区间
在区间![]() 上有界,函数
上有界,函数![]() 叫做有界函数.试探究函数
叫做有界函数.试探究函数![]() (
(![]()
![]()
![]() 是常数)是否是
是常数)是否是![]() (
(![]()
![]() 、
、![]() 是常数)上的有界函数?
是常数)上的有界函数?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建莆田一中高三上学期第一学段考试文科数学试卷(解析版) 题型:填空题
已知定义在 上的偶函数满足:
上的偶函数满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:①
单调递减,给出以下四个命题:① ;②
;② 是函数
是函数 图像的一条对称轴;③函数
图像的一条对称轴;③函数 在区间
在区间 上单调递增;④若方程
上单调递增;④若方程 .在区间
.在区间 上有两根为
上有两根为 ,则
,则 。以上命题正确的是 。(填序号)
。以上命题正确的是 。(填序号)
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高二下学期期末联考(文科)数学卷 题型:填空题
设函数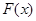 和
和 都在区间
都在区间 上有定义,若对
上有定义,若对 的任意子区间
的任意子区间 ,总有
,总有 上的实数
上的实数 和
和 ,使得不等式
,使得不等式 成立,则称
成立,则称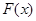 是
是 在区间
在区间 上的甲函数,
上的甲函数, 是
是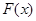 在区间
在区间 上的乙函数.已知
上的乙函数.已知 ,那么
,那么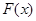 的乙函数
的乙函数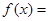 _____________
_____________
查看答案和解析>>
科目:高中数学 来源:2010年上海市松江区高考模拟考试(理) 题型:填空题
设函数 和
和 都在区间
都在区间 上有定义,若对
上有定义,若对 的任意子区间
的任意子区间 ,总有
,总有 上的实数
上的实数 和
和 ,使得不等式
,使得不等式 成立,则称
成立,则称 是
是 在区间
在区间 上的甲函数,
上的甲函数, 是
是 在区间
在区间 上的乙函数.已知
上的乙函数.已知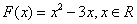 ,那么
,那么 的乙函数
的乙函数 ▲ .
▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com