
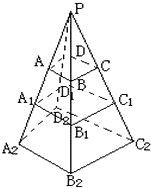
 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比. | a+b |
| 2 |
| S△PBC |
| S△PB1C1 |
| a2 | ||
(
|
| (a+b)2 |
| 4a2 |
| b2 |
| a2 |
| SB1C1CB |
| SB2C2C1B1 |
| S△PB1C1=S△PBC |
| S△PB2C2-S△PB1C1 |
| ||||
|
| b2+2ab-3a2 |
| 3b2-2ab-a2 |
| (b+3a)(b-a) |
| (3b+a)(b-a) |
| b+3a |
| 3b+a |
| SABB1A1 |
| SA1B1B2A1 |
| SDCC1D1 |
| SD1C1C2D2 |
| SADD1A1 |
| SA1D1D2A1 |
| b+3a |
| 3b+a |
| S上棱台侧 |
| S下棱台侧 |
| 3a+b |
| a+3b |
| S上棱台侧 |
| S下棱台侧 |
| 3a+b |
| a+3b |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:《第1章 空间几何体》2013年单元测试卷(12)(解析版) 题型:解答题
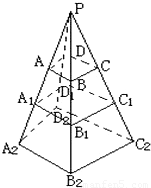 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.查看答案和解析>>
科目:高中数学 来源:《第1章 空间几何体》2013年单元测试卷(4)(解析版) 题型:解答题
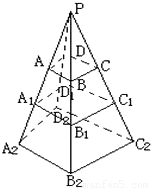 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com