已知f(x)=-2x2+2ax-a2b.
(I)当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值;
(Ⅱ)若对任意实数a,f(2)<0恒成立,求实数b的取值范围;
(Ⅲ)设b使不为0的常数,解关于a的不等式f(1)+ab<0.
【答案】
分析:(I)将不等式f(x)>0的解集为(-1,3),转化为-1,3是方程-2x
2+2ax-a
2b=0的两个根,从而可求a=2,b=
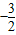
;
(Ⅱ)对任意实数a,f(2)<0恒成立,等价于-8+4a-a
2b0对任意实数a恒成立,从而可求实数b的取值范围;
(Ⅲ)f(1)+ab<0,即-2+2a-a
2b+ab0,对参数b进行讨论,可解不等式.
解答:解:(I)∵不等式f(x)>0的解集为(-1,3),
∴-1,3是方程-2x
2+2ax-a
2b=0的两个根
∴
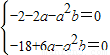
∴a=2,b=
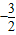
;
(Ⅱ)对任意实数a,f(2)<0恒成立,等价于-8+4a-a
2b<0对任意实数a恒成立
即ba
2-4a+8>0对任意实数a恒成立
∴
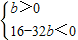
∴
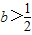
;
(Ⅲ)f(1)+ab<0,即-2+2a-a
2b+ab<0
∴ba
2-(2+b)+2>0
∴(ba-2)(a-1)>0
当b<0时,
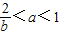
当0<b<2时,a<1,或
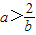
当b=2时a≠1
当b>2时,
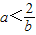
,或a>1
点评:本题以函数为载体,考查不等式解集与方程根的关系,考查二次不等式恒成立问题,考查解不等式,正确分类是关键.

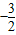 ;
;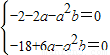
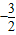 ;
;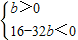
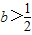 ;
;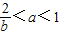
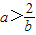
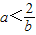 ,或a>1
,或a>1

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案