
【题目】已知定义域为![]() 的函数
的函数![]() (
(![]() ,
,![]() )
)
(1)设![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)设![]() 为
为![]() 导数,
导数,
(i)证明:当![]() ,
,![]() 时,
时,![]() ;
;
(ii)设关于![]() 的方程
的方程![]() 的根为
的根为![]() ,求证:
,求证:![]()
【答案】(1)当![]() 为奇数时
为奇数时![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;当
;当![]() 为偶数时
为偶数时![]() 的增区间为
的增区间为![]() 及
及![]() ,减区间为
,减区间为![]() 。
。
(2)(i)证明见解析,(ii)证明见解析。
【解析】
(1)对![]() ,求导可得
,求导可得![]() ,分当
,分当![]() 为大于1的奇数,和
为大于1的奇数,和![]() 为偶数时两种情况讨论可得
为偶数时两种情况讨论可得![]() 的单调区间;
的单调区间;
(2)(i)设![]() ,
,![]() ,求导得
,求导得![]() ,根据
,根据![]() 研究
研究![]() 即可得到所证结论;
即可得到所证结论;
(ii)![]() ,原方程化为
,原方程化为![]() 解得
解得![]() ,因为
,因为![]() ,所以
,所以![]() ;作差得,
;作差得,![]() ,由(i)知,可得
,由(i)知,可得![]() ,所以
,所以![]() ,即可得证.
,即可得证.
(1)![]() ,
,
当![]() ,
,![]() 时
时![]()
即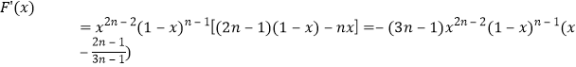
(a)当![]() 为大于1的奇数时,
为大于1的奇数时,![]() 是偶数,
是偶数,![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() ,当
,当![]() 时
时![]()
故![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]()
当![]() 为偶数时,
为偶数时,![]() 是奇数,由于
是奇数,由于![]() ,所以
,所以
当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时
时![]()
故![]() 的增区间为
的增区间为![]() 及
及![]() ,减区间为
,减区间为![]()
综上,当![]() 为奇数时
为奇数时![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,
当![]() 为偶数时
为偶数时![]() 的增区间为
的增区间为![]() 及
及![]() ,减区间为
,减区间为![]() ,
,
(2)(i)证明:设![]() ,
,![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,故
,故![]() 在
在![]() 是增函数,
是增函数,
从而![]() ,由于
,由于![]() ,
,![]()
所以![]() ,
,![]()
所以![]() 在
在![]() 是增函数,
是增函数,![]() ,即
,即![]()
(ii)![]() ,原方程化为
,原方程化为![]()
解得![]() ,因为
,因为![]() ,所以
,所以![]() ;
;
作差得,![]() ,
,
由(i)知,当![]() ,
,![]() 时,
时,![]() ,
,
令![]() ,
,![]() ,故有
,故有![]() ,所以
,所以![]() ,
,![]() ,
,
综上,![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 图象上两相邻对称轴之间的距离为
图象上两相邻对称轴之间的距离为![]() ;_______________;
;_______________;
(Ⅰ)在①![]() 的一条对称轴
的一条对称轴![]() ;②
;②![]() 的一个对称中心
的一个对称中心![]() ;③
;③![]() 的图象经过点
的图象经过点![]() 这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
(Ⅱ)若动直线![]() 与
与![]() 和
和![]() 的图象分别交于
的图象分别交于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最大值及此时
长度的最大值及此时![]() 的值.
的值.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
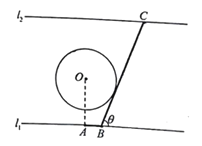
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
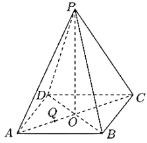
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
①记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
②在区间![]() 内任取2个实数
内任取2个实数![]() ,
,![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2cos(2x+![]() )的图象向左平移
)的图象向左平移![]() 个单位长度,得到函数y=f(x)的图象.
个单位长度,得到函数y=f(x)的图象.
(1)求f(x)的单调递增区间;
(2)求f(x)在[0,![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年春节,各地的餐馆都出现了用餐需预定的现象,致使一些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们的用餐地点及性别作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
男性 | 30 | ||
女性 | 40 | ||
总计 | 50 | 100 |
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明用餐地点与性别有关?
的把握说明用餐地点与性别有关?
参考公式及数据: ,其中
,其中![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善市民的生活环境,长沙某大型工业城市决定对长沙市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现长沙市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
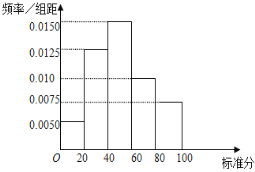
(Ⅰ)如图为长沙市的某工业区所有被调査的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调査的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(Ⅱ)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com