
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或 ![]() ,则f(ex)>0的解集为( )
,则f(ex)>0的解集为( )
A.{x|x<﹣1或x>﹣ln3}
B.{x|﹣1<x<﹣ln3}
C.{x|x>﹣ln3}
D.{x|x<﹣ln3}
【答案】D
【解析】解:∵一元二次不等式f(x)<0的解集为{x|x<﹣1或x> ![]() },
},
∴﹣1和 ![]() 是方程x2+ax+b=0的两个实数根,
是方程x2+ax+b=0的两个实数根,
∴a=﹣(﹣1+ ![]() )=
)= ![]() ,
,
b=﹣1× ![]() =﹣
=﹣ ![]() ,
,
∴f(x)=﹣(x2+ ![]() x﹣
x﹣ ![]() )=﹣x2﹣
)=﹣x2﹣ ![]() x+
x+ ![]() ;
;
∴不等式f(ex)>0可化为
e2x+ ![]() ex﹣
ex﹣ ![]() <0,
<0,
解得﹣1<ex< ![]() ,
,
即x<ln ![]() ,
,
∴x<﹣ln3,
即f(ex)>0的解集为{x|x<﹣ln3}.
故选:D.
【考点精析】本题主要考查了解一元二次不等式的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立,则实数a的取值范围是( )
A.(﹣∞,1]
B.[0,1]
C.![]()
D.[0,e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数满足x2﹣4ax+3a2<0,a≠0;命题q:实数满足 ![]() ≥0.
≥0.
(1)若a=1,p∧q为真命题,求x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或x> ![]() },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )
A.{x|x<﹣1或x>﹣lg2}
B.{x|﹣1<x<﹣lg2}
C.{x|x>﹣lg2}
D.{x|x<﹣lg2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(x+1)+a(x2﹣x),a≥0.
(1)当a=1时,求函数f(x)的极值;
(2)若x>0,f(x)≥0成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. 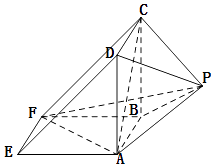
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com