【题目】已知P为△ABC内一点，且满足 
，记△ABP，△BCP，△ACP的面积依次为S1 ， S2 ， S3 ， 则S1：S2：S3等于（ ）
A.1：2：3
B.1：4：9
C.2：3：1
D.3：1：2
【答案】D
【解析】解：如图：设D、E 分别为BC、AC的中点， ∵ 
=0，∴ 
﹣ 
=﹣3（ + 
），
∴ 
=﹣3×2 =﹣6 ，
同理由（ + ）=﹣2（ + ），即 2 
=﹣2× ，
∴ =﹣ 
．∴P到BC的距离等于A到BC的距离的 
，
设△ABC的面积为S，则S2 = S．
P到AC的距离等于B到AC的距离的 ，
∴S3 = S．∴S1 =S﹣S2﹣S3 = 
S．
∴S1：S2：S3= S： S= S=3：1：2，
故选D．
根据已知的等式变形可得 =﹣6 ， =﹣ ，从而得出P到BC的距离等于A到BC的距离的 ，P到AC的距离等于B到AC的距离的 ．从而有S2 = S，S3 = S，S1 =S﹣S2﹣S3 = S即可解决问题．
科目：高中数学 来源： 题型：
【题目】已知Sn为等比数列{an}的前n项和且S4=S3+3a3 ， a2=9．
（1）求数列{an}的通项公式
（2）设bn=（2n﹣1）an ， 求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC= 
，O，M分别为AB，VA的中点．
（1）求证：VB∥平面MOC；
（2）求证：平面MOC⊥平面VAB
（3）求三棱锥V﹣ABC的体积．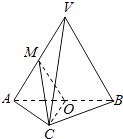 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设A、B分别为双曲线 
的左右顶点，双曲线的实轴长为4 
，焦点到渐近线的距离为 ．
（1）求双曲线的方程；
（2）已知直线 
与双曲线的右支交于M、N两点，且在双曲线的右支上存在点D，使 
，求t的值及点D的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜，我艇立即以14海里/小时的速度追击，求我艇追上走私船所需要的最短时间．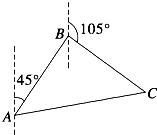 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆E： 
=1（a＞b＞0）的离心率为 
，过焦点垂直与x轴的直线被椭圆E截得的线段长为 
．
（1）求椭圆E的方程；
（2）斜率为k的直线l经过原点，与椭圆E相交于不同的两点M，N，判断并说明在椭圆E上是否存在点P，使得△PMN的面积为 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知公差不为0的等差数列{an}中，a1=2，且a2+1，a4+1，a8+1成等比数列．
（1）求数列{an}通项公式；
（2）设数列{bn}满足bn= 
，求适合方程b1b2+b2b3+…+bnbn+1= 
的正整数n的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知点D为△ABC的边BC上一点， 
=3 
，En（n∈N+）为边AC上的点，满足 
= 
an+1 ， 
=（4an+3） 
，其中实数列{an}中an＞0，a1=1，则{an}的通项公式为（ ） 
A.32n﹣1﹣2
B.2n﹣1
C.4n﹣2
D.24n﹣1﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
