Question

一海豚在水池中自由游弋,水池为长30 m,宽20 m的长方形,求此刻海豚嘴尖离岸边不超过2 m的概率；并利用计算机或计算器模拟试验.

Answer 1

【探究】海豚在水中自由游弋,其在水池中的哪个位置是等可能的,故这是几何概型.

【解法一】对于几何概型,关键是要构造出随机事件对应的几何图形,利用图形的几何度量来求随机事件的概率.如图3-3-19所示,区域Ω是长30 m、宽20 m的长方形.图中阴影部分表示事件A：“海豚嘴尖离岸边不超过2 m”,问题可以理解为求海豚嘴尖出现在图中阴影部分的概率.由于区域Ω的面积为30×20=600(m²),

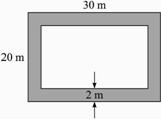
             图3-3-19

    阴影A的面积为30×20-26×16=184(m²).

∴P(A)=≈0.31.

【解法二】利用计算机产生随机数x和y,用它们来表示海豚嘴尖的横坐标与纵坐标.

    下面设计一个算法使得计算机或计算器能模拟这个试验,并且估计事件A发生的概率.

    第一步：用计数器n记录做了多少次试验,用计数器m记录其中有多少次(x,y)出现在阴影部分中.首先置n=0,m=0.

    第二步：用变换rand(#)*30-15产生-15—15之间的随机数x作为海豚嘴尖的横坐标；用变换rand(#)*20-10产生-10—10之间的随机数y作为海豚嘴尖的纵坐标.

    第三步：判断(x,y)是否落在阴影部分中,即是否满足||x|-15|≤2或||y|-10|≤2.如果是,则计数器m的值加1,即m=m+1.如果不是,m的值保持不变.

    第四步：表示随机试验次数的计数器n的值加1,即n=n+1.如果还需要继续试验,则返回第二步继续执行,否则程序结束.程序结束后事件A发生的频率mn作为A的概率的近似值.

规律总结 均匀随机数在日常生活中,有着广泛的应用,我们可以利用计算器或计算机来产生均匀随机数,从而来模拟随机试验,其具体方法是：建立一个概率模型,它与某些我们感兴趣的量(如概率值、常数π)有关,然后设计适当的试验,并通过这个试验的结果来确定这些量.