
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)函数![]() 的图象能否与
的图象能否与![]() 轴相切?若能,求出实数a,若不能,请说明理由;
轴相切?若能,求出实数a,若不能,请说明理由;
(Ⅱ)求最大的整数![]() ,使得对任意
,使得对任意![]() ,不等式
,不等式![]()
恒成立.
【答案】(1)不能(2)![]()
【解析】试题分析:
(Ⅰ)假设函数![]() 的图象能与
的图象能与![]() 轴相切.设切点为
轴相切.设切点为![]() ,根据导数的几何意义得到关于
,根据导数的几何意义得到关于![]() 的方程,然后判断此方程是否有解即可得到结论.(Ⅱ)将不等式变形为
的方程,然后判断此方程是否有解即可得到结论.(Ⅱ)将不等式变形为![]() ,设
,设![]() ,则问题等价于
,则问题等价于![]() 对任意
对任意![]() 恒成立,故只需函数
恒成立,故只需函数![]() 在R上单调递增,因此
在R上单调递增,因此![]() 在R上恒成立即可,由
在R上恒成立即可,由![]() 可得
可得
![]() ,即为
,即为![]() 成立的必要条件,然后再证
成立的必要条件,然后再证![]() 时,
时,![]() 即可得到结论.
即可得到结论.
试题解析:
(Ⅰ)∵![]() ,
,
∴![]() .
.
假设函数![]() 的图象与
的图象与![]() 轴相切于点
轴相切于点![]() ,
,
则有![]() , 即
, 即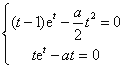 .
.
显然![]() ,将
,将![]() 代入方程
代入方程![]() 中可得
中可得![]() .
.
∵![]() ,
,
∴方程![]() 无解.
无解.
故无论a取何值,函数![]() 的图象都不能与
的图象都不能与![]() 轴相切.
轴相切.
(Ⅱ)由题意可得原不等式可化为![]() ,
,
故不等式![]() 在R上恒成立.
在R上恒成立.
设![]() ,则上式等价于
,则上式等价于![]() ,
,
要使![]() 对任意
对任意![]() 恒成立,
恒成立,
只需函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恒成立.
上恒成立.
则![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上恒成立的必要条件是:
上恒成立的必要条件是:![]() .
.
下面证明:当![]() 时,
时,![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴![]() ,即
,即![]() .
.
则当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
∴![]() 恒成立.
恒成立.
所以实数![]() 的最大整数值为3.
的最大整数值为3.


科目:高中数学 来源: 题型:
【题目】某老师对全班![]() 名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 |
| ||
学习积极性一般 |
| ||
合计 |
|
|
(1)请把表格数据补充完整;
(2)若从不参加社团活动的![]() 人按照分层抽样的方法选取
人按照分层抽样的方法选取![]() 人,再从所选出的
人,再从所选出的![]() 人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
(3)运用独立性检验的思想方法分析:请你判断是否有![]() 的把握认为学生的学习积极性与参与社团活动由关系?
的把握认为学生的学习积极性与参与社团活动由关系?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率为
的中心在原点,离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆下顶点为![]() ,直线
,直线![]() (
(![]() )与椭圆相交于不同的两点
)与椭圆相交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若曲线![]() 与曲线
与曲线![]() 在公共点处有共同的切线,求实数
在公共点处有共同的切线,求实数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问函数![]() 是否有零点?如果有,求出该零点;若没有,请说明理由.
是否有零点?如果有,求出该零点;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
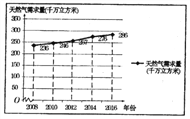
【题目】2017年12月,针对国内天然气供应紧张的问题,某市政府及时安排部署,加气站采取了紧急限气措施,全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况,对该地区某些年份天然气需求量进行了统计,并绘制了相应的折线图.
(Ⅰ)由折线图可以看出,可用线性回归模型拟合年度天然气需求量![]() (单位:千万立方米)与年份
(单位:千万立方米)与年份![]() (单位:年)之间的关系.并且已知
(单位:年)之间的关系.并且已知![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,试确定
,试确定![]() 的值,并预测2018年该地区的天然气需求量;
的值,并预测2018年该地区的天然气需求量;
(Ⅱ)政府部门为节约能源出台了《购置新能源汽车补贴方案》,该方案对新能源汽车的续航里程做出了严格规定,根据续航里程的不同,将补贴金额划分为三类,A类:每车补贴1万元,B类:每车补贴2.5万元,C类:每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计,结果如下表:
![]()
为了制定更合理的补贴方案,政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况,在该出租车公司的60辆车中抽取6辆车作为样本,再从6辆车中抽取2辆车进一步跟踪调查,求恰好有1辆车享受3.4万元补贴的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
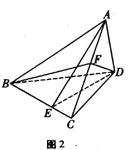
【题目】如图2,在三棱锥A-BCD中,AB=CD=4, AC=BC=AD=BD=3.
(I)证明:AB![]() CD;
CD;
(II) E在线段BC上,BE=2EC, F是线段AC的中点,求平面ADE与平面BFD所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】试题分析:(1)根据题意![]() ,
, ![]() ,
, ![]() 成等比数列得
成等比数列得![]() 得
得![]() 求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得
求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 计算 即可得出结论
计算 即可得出结论
解析:(1)由题意可得,则![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 时,
时,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
点睛:对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决,对于第二问前n项的绝对值的和问题,首先要找到数列由多少正数项和负数项,进而找到绝对值所影响的项,然后在求解即可得结论
【题型】解答题
【结束】
18
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com