
【题目】在![]() 中,内角A,B,C的对边分别为a,b,c,且
中,内角A,B,C的对边分别为a,b,c,且![]() .
.
(1)若![]() ,
,![]() ,请判断
,请判断![]() 的形状;
的形状;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列![]() 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使数列
,使数列![]() 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
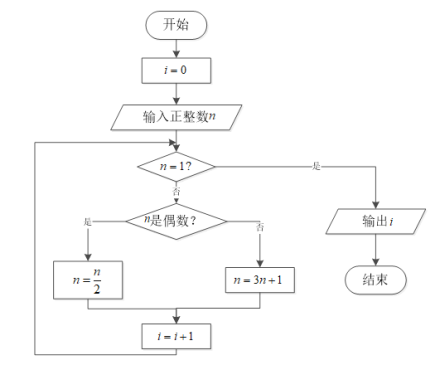
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 和圆
和圆![]() 均内切.
均内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于
且垂直于![]() 的直线交轨迹
的直线交轨迹![]() 于两点
于两点![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上是减函数,
上是减函数,![]() ,
,![]() 现有下列结论,其中正确的是:( )
现有下列结论,其中正确的是:( )
①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的图象关于点
的图象关于点![]() 对称;③
对称;③![]() 在区间
在区间![]() 上是减函数;④
上是减函数;④![]() 在区间
在区间![]() 内有8个零点.
内有8个零点.
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试研究,一个三角形能否同时具有以下两个性质:(1)三边是连续的三个自然数;(2)最大角是最小角的2倍.若能,请求出这个三角形的三边以及最大角的余弦值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com