
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
科目:高中数学 来源: 题型:
【题目】某投资公司拟投资开发某项新产品,市场评估能获得10~1 000万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不低于1万元,同时不超过投资收益的20%.
(1) 设奖励方案的函数模型为f(x),试用数学语言表述公司对奖励方案的函数模型f(x)的基本要求;
(2) 公司能不能用函数f(x)=![]() +2作为预设的奖励方案的模型函数?
+2作为预设的奖励方案的模型函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
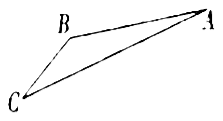
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图5所示:将
的一段图象如图5所示:将![]() 的图像向右平移
的图像向右平移![]() 个单位,可得到函数
个单位,可得到函数![]() 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,

(1)求![]() 的值;
的值;
(2)求![]() 的最小值,并写出
的最小值,并写出![]() 的表达式;
的表达式;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上最小值为
上最小值为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 若给变量x一个值,由回归直线方程![]() =0.85x-85.71得到一个
=0.85x-85.71得到一个![]() ,则
,则![]() 为该统计量中的估计值
为该统计量中的估计值
C. 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:指数函数y=(1-a)x是R上的增函数,命题q:不等式ax2+2x-1>0有解.若命题p是真命题,命题q是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列方程,并回答问题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;…
;…
(1)请你根据这列方程的特点写出第![]() 个方程;
个方程;
(2)直接写出第2009个方程的根;
(3)说出这列方程的根的一个共同特点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于
轴负半轴于![]() 点,且
点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若过![]() 、
、![]() 、
、![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(3)过![]() 的直线
的直线![]() 与(2)中椭圆交于不同的两点
与(2)中椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com