Question

已知正方体ABCD-A₁B₁C₁D₁，其棱长为2，O是底ABCD对角线的交点．
求证：（1）C₁O∥面AB₁D₁；
（2）A₁C⊥面AB₁D₁．
（3）若M是CC₁的中点，求证：平面AB₁D₁⊥平面MB₁D₁．

Answer 1

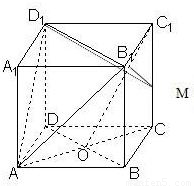
【答案】分析：（1）连接A₁C₁，设A₁C₁∩B₁D₁=O₁连接AO₁，由正方体的几何特征，我们易得到C₁O∥AO₁，结合线面平行的判定定理，即可得到C₁O∥面AB₁D₁；
（2）由正方体的几何特征，我们可得CC₁⊥面A₁B₁C₁D₁，进而得到A₁C⊥B₁D₁及A₁C⊥AB₁，由线面垂直的判定定理，即可得到A₁C⊥面AB₁D₁．
（3）若M是CC₁的中点，设B₁D₁的中点为N，则AN⊥B₁D₁，MN⊥B₁D₁，由勾股定理，我们可以判断出△AMN是RT△，进而根据面面垂直的判定定理得到平面AB₁D₁⊥平面MB₁D₁．
解答：证明：（1）连接A₁C₁，设A₁C₁∩B₁D₁=O₁，连接AO₁，
∵ABCD-A₁B₁C₁D₁是正方体
∴A₁ACC₁是平行四边形
∴A₁C₁∥AC且A₁C₁=AC
又O₁，O分别是A₁C₁，AC的中点，
∴O₁C₁∥AO且O₁C₁=AO
∴AOC₁O₁是平行四边形
∴C₁O∥AO₁，AO₁?面AB₁D₁，C₁O?面AB₁D₁
∴C₁O∥面AB₁D₁（5分）
（2）∵CC₁⊥面A₁B₁C₁D₁
∴CC₁⊥B₁D_!
又∵A₁C₁⊥B₁D₁，
∴B₁D₁⊥面A₁C₁C
即A₁C⊥B₁D₁
同理可证A₁C⊥AB₁，
又D₁B₁∩AB₁=B₁
∴A₁C⊥面AB₁D₁（9分）
（3）设B₁D₁的中点为N，则AN⊥B₁D₁，MN⊥B₁D₁，
则
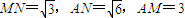
∴AN²+MN²=AM²，
∴△AMN是RT△，
∴AN⊥MN，
∴AN⊥面MB₁D₁，
∴面AB₁D₁⊥面MB₁D₁．
点评：本题考查的知识点是平面与平面垂直的判定，直线与平面平行的判定，直线与平面垂直的性质，属于空间直线与平面间关系判定定理及性质定理的基本应用．