
【题目】如图,在正方形ABCD的一边CD内任取一点E,过E作对角线AC的平行线,交对角线BD于点G、交边AD于点H、交边BA的延长线于点F,联结BH交DF于点M.求证:
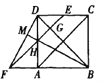
(1)C、G、M三点共线;
(2)C、E、M、F四点共圆.
科目:高中数学 来源: 题型:
【题目】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有三种类型的纸片(可翻转)。
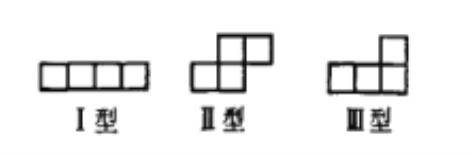
证明:(1)当![]() 时,
时,![]() 的纸板不能分割成若干个I型、II型的纸片;
的纸板不能分割成若干个I型、II型的纸片;
(2)当n为大于2的偶数时,![]() 的纸板可以分割成若干个II型、III型的纸片。
的纸板可以分割成若干个II型、III型的纸片。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一.在欧洲,左下图叫帕斯卡三角形,帕斯卡在1654年发现的这一规律,比杨辉要迟393年,比贾宪迟600年.某大学生要设计一个程序框图,按右下图标注的顺序将表上的数字输出,若第5次输出数“1”后结束程序,则空白判断框内应填入的条件为( )
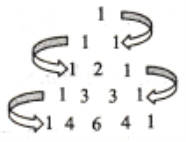
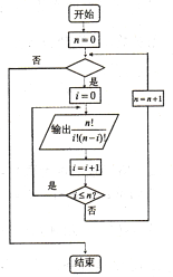
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 为抛物线
为抛物线![]() :
:![]() 上两点,
上两点,![]() 为抛物线焦点.分别过
为抛物线焦点.分别过![]() ,
,![]() 作抛物线的切线交于点
作抛物线的切线交于点![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 分别交
分别交![]() 轴于
轴于![]() ,
,![]() 两点,试问
两点,试问![]() 的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项.来自100多个国家的近万名现役军人同台竞技.军运会召开前,为迎接军运会顺利召开,武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动,努力让大家更多的了解军运会的相关知识,并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况,在全市开展了网上问卷调查,民众参与度极高,现从大批参与者中随机抽取200名幸运参与者,他们得分(满分100分)数据,统计结果如下:
组别 | (30,40) | (40,50) | (50,60) | (60,70) | (70,80) | (80,90) | (90,100) |
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次问卷调查得分X整体服从正态分布![]() ,用样本来估计总体,设
,用样本来估计总体,设![]() ,
,![]() 分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),
分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),
①求![]() 的值;
的值;
②经计算![]() ,求
,求![]() 的值.
的值.
(2)在(1)的条件下,为感谢大家参与这次活动,市体育局还对参加问卷调查的幸运市民制定如下奖励方案:得分低于![]() 的可以获得1次抽奖机会,得分不低于
的可以获得1次抽奖机会,得分不低于![]() 的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品
的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品![]()
![]() ;抽中价值为30元的纪念品
;抽中价值为30元的纪念品![]() 的概率为
的概率为![]() ,现有市民张先生参加了此次问卷调查并成为幸运参与者,记
,现有市民张先生参加了此次问卷调查并成为幸运参与者,记![]() 为他参加活动获得纪念品的总价值,求
为他参加活动获得纪念品的总价值,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:若![]() ,则
,则![]() ,
,![]() .
.![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知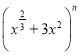 展开式中,各项系数和比它的二项式系数和大992,则下列结论正确的是( )
展开式中,各项系数和比它的二项式系数和大992,则下列结论正确的是( )
A.展开式中的有理项是第2项和第5项B.展开式中没有常数项
C.展开式中二项式系数最大的项是第3项和第4项D.展开式中系数最大的项是第5项
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com