
【题目】假设A型进口车关税税率在2002年是100%,在2007年是25%,2002年A型进口车每辆价格为64万元(其中含32万元关税税款)
(1)已知与A型车性能相近的B型国产车,2002年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2007年B型车的价格不高于A型车价格的90%,B型车价格要逐年减低,问平均每年至少下降多少万元?
(2)某人在2002年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带息是否一定够买按(1)中所述降价后的B型车一辆?
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() (
(![]() 为常数,
为常数,![]() ,
,![]() ,
,![]() ),给出下列四个结论:①若数列
),给出下列四个结论:①若数列![]() 是周期数列,则周期必为2:②若
是周期数列,则周期必为2:②若![]() ,则数列
,则数列![]() 必是常数列:③若
必是常数列:③若![]() ,则数列
,则数列![]() 是递增数列:④若
是递增数列:④若![]() ,则数列
,则数列![]() 是有穷数列,其中,所有错误结论的序号是________.
是有穷数列,其中,所有错误结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 轴的上方,且点
轴的上方,且点![]() 的横坐标为4.
的横坐标为4.
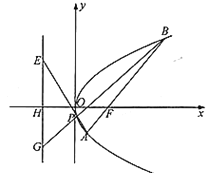
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设点![]() 为抛物线
为抛物线![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 与
与![]() 分别交抛物线
分别交抛物线![]() 的准线于
的准线于![]() ,
,![]() 两点,
两点,![]() 轴与准线的交点为
轴与准线的交点为![]() ,求证:
,求证:![]() 为定值,并求出定值.
为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳![]() 元(
元(![]() 为常数,
为常数,![]() )的管理费.根据多年的统计经验,预计当每件产品的售价为
)的管理费.根据多年的统计经验,预计当每件产品的售价为![]() 元时,产品一年的销售量为
元时,产品一年的销售量为![]() 为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价
为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价![]() 最低不低于35元,最高不超过41元.
最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润![]() 万元与每件产品的售价
万元与每件产品的售价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润![]() 最大,并求
最大,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B为曲线C:![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com