
【题目】设A,B为曲线C:![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
【答案】(1)1;(2)y=x+7..
【解析】
(1)设![]() 两点坐标,代入抛物线方程 相减后可求得
两点坐标,代入抛物线方程 相减后可求得![]() 的斜率;
的斜率;
(2)由C在M处的切线与直线AB平行,可求得切点![]() 坐标,设直线AB的方程为y=x+m,代入抛物线方程可得
坐标,设直线AB的方程为y=x+m,代入抛物线方程可得![]() 中点为
中点为![]() ,AM⊥BM等价于
,AM⊥BM等价于![]() ,这样可求得
,这样可求得![]() 值.
值.
解:(1)设A(x1,y1),B(x2,y2),则x1≠x2,![]() ,x1+x2=4,于是直线AB的斜率
,x1+x2=4,于是直线AB的斜率![]() .
.
(2)由![]() ,得
,得![]() .
.
设M(x3,y3),由题设知![]() ,解得x3=2,于是M(2,1).
,解得x3=2,于是M(2,1).
设直线AB的方程为y=x+m,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
将y=x+m代入![]() 得x2-4x-4m=0.
得x2-4x-4m=0.
当Δ=16(m+1)>0,即m>-1时,![]() .
.
从而![]() .
.
由题设知|AB|=2|MN|,即![]() ,解得m=7.
,解得m=7.
所以直线AB的方程为y=x+7.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】假设A型进口车关税税率在2002年是100%,在2007年是25%,2002年A型进口车每辆价格为64万元(其中含32万元关税税款)
(1)已知与A型车性能相近的B型国产车,2002年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2007年B型车的价格不高于A型车价格的90%,B型车价格要逐年减低,问平均每年至少下降多少万元?
(2)某人在2002年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带息是否一定够买按(1)中所述降价后的B型车一辆?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大城市往往人口密集,城市绿化在健康人民群众肺方面发挥着非常重要的作用,历史留给我们城市里的大山拥有品种繁多的绿色植物更是无价之宝.改革开放以来,有的地方领导片面追求政绩,对森林资源野蛮开发受到严肃查处事件时有发生.2019年的春节后,广西某市林业管理部门在“绿水青山就是金山银山”理论的不断指引下,积极从外地引进甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:
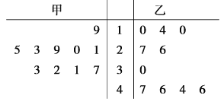
(1)据茎叶图求甲、乙两种树苗的平均高度;
(2)据茎叶图,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为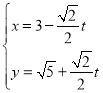 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(1)求椭圆的方程;
(2)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求证:直线
,求证:直线![]() 的斜率与直线MN的斜率之积为定值.
的斜率与直线MN的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于M.N点.
的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于M.N点.
(1)若![]() ,
,![]() 的面积为
的面积为![]() ,求抛物线方程;
,求抛物线方程;
(2)若A.M.F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到直线n、m距离的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com