
【题目】给定数列![]() ,若数列
,若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,试判断
,试判断![]() 是否为封闭数列,并说明理由;
是否为封闭数列,并说明理由;
(2)已知数列![]() 满足
满足![]() 且
且![]() ,设
,设![]() 是该数列
是该数列![]() 的前
的前![]() 项和,试问:是否存在这样的“封闭数列”
项和,试问:是否存在这样的“封闭数列”![]() ,使得对任意
,使得对任意![]() 都有
都有![]() ,且
,且![]() ,若存在,求数列
,若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由;
的所有取值;若不存在,说明理由;
(3)证明等差数列![]() 成为“封闭数列”的充要条件是:存在整数
成为“封闭数列”的充要条件是:存在整数![]() ,使
,使![]() .
.
【答案】(1)不是;见解析(2)![]() 或
或![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)数列![]() 不为封闭数列.由
不为封闭数列.由![]() ,2时,
,2时,![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() ,即可得出结论.
,即可得出结论.
(2)数列![]() 满足
满足![]() 且
且![]() ,可得数列
,可得数列![]() 为等差数列,公差为2.
为等差数列,公差为2.![]() .又
.又![]() 是“封闭数列”,得:对任意
是“封闭数列”,得:对任意![]() ,
,![]() ,必存在
,必存在![]() 使
使![]() ,得
,得![]() ,故
,故![]() 是偶数,又由已知,
是偶数,又由已知,![]() ,故
,故![]() ,可得
,可得![]() .
.
(3)要证明充分必要条件的问题,本题需要从两个方面来证明,一是证明充分性,二是证明必要性,证明时注意所取得数列的项来验证时,项要具有一般性.
解:(1)数列![]() 不为封闭数列.
不为封闭数列.
∵![]() ,2时,
,2时,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,∴
,∴![]() ,因此
,因此![]() 不是封闭数列.
不是封闭数列.
(2)数列![]() 满足
满足![]() 且
且![]() ,
,
∴数列![]() 是以2为公差的等差数列,则
是以2为公差的等差数列,则![]() .
.
又![]() 是“封闭数列”,
是“封闭数列”,
∴对任意![]() ,
,![]() ,必存在
,必存在![]() 使
使![]() ,
,
得![]() ,故
,故![]() 是偶数,
是偶数,
又由已知,![]() ,故
,故![]() ,可得:
,可得:![]() ,
,
可得![]() 或
或![]() 或
或![]() ,
,
经过验证可得:![]() 或
或![]() .
.
(3)证明:(必要性)若存在整数![]() ,使
,使![]() ,则任取等差数列的两项
,则任取等差数列的两项![]() ,
,![]() ,
,
于是![]() ,
,
由于![]() ,
,![]() ,
,![]() 为正整数,
为正整数,![]() ,
,
![]() 是封闭数列.
是封闭数列.
(充分性)任取等差数列的两项![]() ,
,![]() ,若存在
,若存在![]() 使
使![]() ,
,
则![]() ,
,
故存在![]() ,使
,使![]() ,
,
下面证明![]() .
.
当![]() 时,显然成立.
时,显然成立.
对![]() ,若
,若![]() ,则取
,则取![]() ,对不同的两项
,对不同的两项![]() 和
和![]() ,存在
,存在![]() 使
使![]() ,
,
即![]() ,这与
,这与![]() ,
,![]() 矛盾,
矛盾,
故存在整数![]() ,使
,使![]() .
.


科目:高中数学 来源: 题型:
【题目】我们在求高次方程或超越方程的近似解时常用二分法求解,在实际生活中还有三分法.比如借助天平鉴别假币.有三枚形状大小完全相同的硬币,其中有一假币(质量较轻),把两枚硬币放在天平的两端,若天平平衡,则剩余一枚为假币,若天平不平衡,较轻的一端放的硬币为假币.现有 27 枚这样的硬币,其中有一枚是假币(质量较轻),如果只有一台天平,则一定能找到这枚假币所需要使用天平的最少次数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点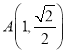 ,且以
,且以![]() ,
,![]()
![]() 为焦点,椭圆
为焦点,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求实数![]() 的值;
的值;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,问椭圆
为坐标原点,问椭圆![]() 上是否存在点
上是否存在点![]() ,使线段
,使线段![]() 和线段
和线段![]() 相互平分?若存在,求出点
相互平分?若存在,求出点![]() 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国和印度是当今世界上两个发展最快且是最大的发展中国家,为了解两国经济的发展情况,收集了2008年至2017年两国GDP年度增长率,并绘制成如图折线图,则下列结论不正确的是( )
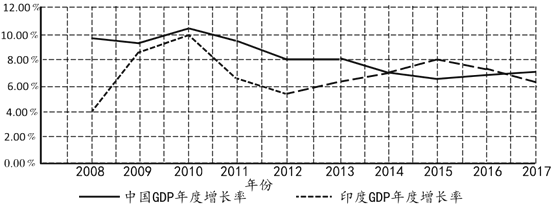
A.2010年,两国GDP年度增长率均为最大
B.2014年,两国GDP年度增长率几乎相等
C.这十年内,中国比印度的发展更为平稳一些
D.2015年起,印度GDP年度增长率均比中国大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com