
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
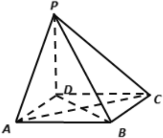
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据菱形对角线互相垂直及![]() 平面ABCD,由线面垂直的判定定理得到
平面ABCD,由线面垂直的判定定理得到![]() 平面PBD;
平面PBD;
(2)可直接作出线面角用几何法求之,也可建立空间直角坐标系用向量法求之.
(Ⅰ)![]() 底面ABCD是平行四边形且
底面ABCD是平行四边形且![]() ,
,
![]() 是菱形,即
是菱形,即![]() ,
,
又![]() 平面ABCD,得
平面ABCD,得![]() ,
,
所以![]() 平面PBD.
平面PBD.
(Ⅱ)方法一(几何法):
取BC的中点Q,
连结PQ,DQ,交AC于点G,
过点G作![]() ,连HC,
,连HC,
![]() 在平行四边形ABCD中
在平行四边形ABCD中![]() 且
且![]()
![]() 是正三角形,即点G为重心,
是正三角形,即点G为重心,
又![]() 平面ABCD,得
平面ABCD,得![]() ,又
,又![]() ,
,
即![]() 平面PDQ,所以面
平面PDQ,所以面![]() 面PDQ,
面PDQ,
由作法知,![]() 平面PBC,
平面PBC,
所以![]() 就是直线AC与平面PBC所成的角,
就是直线AC与平面PBC所成的角,
设![]() ,则
,则![]() ,再由相似求得
,再由相似求得![]()
在![]() ,
,![]() ,
,
所以直线AC与平面PBC所成角的正弦值是![]() .
.
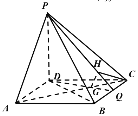
方法二(坐标法):
取PB的中点Q,以O为原点,分别以OA,OB,OQ为轴建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面PBC法向量![]() ,
,
则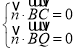 ,
,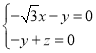
取![]() ,
,
记直线AC与平面PBC所成角为![]() ,
,
得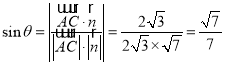 ,
,
所以直线AC与平面PBC所成角的正弦值是![]() .
.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+acosx.
(1)求函数f(x)的奇偶性.并证明当|a|≤2时函数f(x)只有一个极值点;
(2)当a=π时,求f(x)的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:万元/平方米,
(单位:万元/平方米,![]() 进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价
进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价![]() (单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
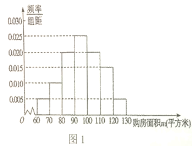
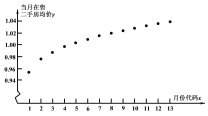
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房面积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如下表所示:
,并得到一些统计量的值,如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.00050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: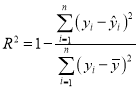 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到其中所有正确结论的编号是( )
个单位得到其中所有正确结论的编号是( )
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1F2,右顶点为A,P为椭圆C上任意一点.已知
的左右焦点分别为F1F2,右顶点为A,P为椭圆C上任意一点.已知![]() 的最大值为3,最小值为2.
的最大值为3,最小值为2.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C相交于MN两点(MN不是左右顶点),且以MN为直径的圆过点A.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了![]() 位患者和
位患者和![]() 位非患者,用该试剂盒分别对他们进行检测,结果如下:
位非患者,用该试剂盒分别对他们进行检测,结果如下:
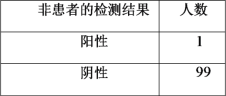
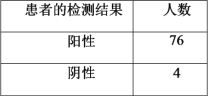
(1)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(2)从该地区患者中随机选取![]() 人,各检测一次,假设每位患者的检测结果相互独立,以
人,各检测一次,假设每位患者的检测结果相互独立,以![]() 表示检测结果为阳性的患者人数,利用(1)中所得概率,求
表示检测结果为阳性的患者人数,利用(1)中所得概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)假设该地区有![]() 万人,患病率为
万人,患病率为![]() .从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过
.从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com