
【题目】函数f(x)=a+ ![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
(1)求a的值;
(2)判断函数f(x)在(﹣∞,+∞)的单调性并给予证明.
【答案】
(1)
解:∵函数 ![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
∴f(0)=0,
即 ![]() ,解得
,解得 ![]()
(2)
解:由(1)知 ![]() ,则
,则 ![]() ,
,
函数f(x)在(﹣∞,+∞)上单调递减,给出如下证明:
证法一:任取x1,x2∈(﹣∞,+∞),且x1<x2,
则 ![]()
= ![]() =
= ![]() )
)
= ![]() ,
,
∵x1<x2,∴x2﹣x1>0,∴ ![]() ,∴
,∴ ![]() ,
,
又∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() >0,即f(x2)﹣f(x1)>0,
>0,即f(x2)﹣f(x1)>0,
∴f(x2)>f(x1),
∴函数f(x)在(﹣∞,+∞)上单调递减.
证法二:∵ ![]()
∴ ![]() ,
,
∵f′(x)<0恒成立,
故函数f(x)在(﹣∞,+∞)上单调递减.
【解析】(1)函数 ![]() 为定义在R上的奇函数.则f(0)=0,解得a的值;(2)证法一:任取x1 , x2∈(﹣∞,+∞),且x1<x2 , 作差判断f(x2)与f(x1)的大小,结合单调性的定义,可得函数f(x)在(﹣∞,+∞)的单调性;
为定义在R上的奇函数.则f(0)=0,解得a的值;(2)证法一:任取x1 , x2∈(﹣∞,+∞),且x1<x2 , 作差判断f(x2)与f(x1)的大小,结合单调性的定义,可得函数f(x)在(﹣∞,+∞)的单调性;
证法二:求导,判断导函数的符号,进而可得函数f(x)在(﹣∞,+∞)的单调性.
【考点精析】本题主要考查了函数单调性的判断方法和函数奇偶性的性质的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:函数y=log2(x2﹣2x)的单调增区间是[1,+∞),命题q:函数y=![]() 的值域为(0,1),下列命题是真命题的为( )
的值域为(0,1),下列命题是真命题的为( )
A.p∧q
B.p∨q
C.p∧(¬q)
D.¬q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e﹣x , 其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x|0≤x≤2},N={y|0≤y≤2},从M到N有四种对应如图所示: 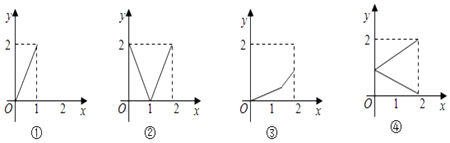
其中能表示为M到N的映射关系的有(请填写符合条件的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项的和记为Sn . 如果a4=﹣12,a8=﹣4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com